题目内容
14. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).则正方形ABCD的面积为5,延长CB交x轴于点A1,作正方形A1B1C1C,则正方形A1B1C1C的面积为$\frac{45}{4}$;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,正方形A2015B2015C2015C2014的面积为5×${({\frac{9}{4}})^{2015}}$.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).则正方形ABCD的面积为5,延长CB交x轴于点A1,作正方形A1B1C1C,则正方形A1B1C1C的面积为$\frac{45}{4}$;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,正方形A2015B2015C2015C2014的面积为5×${({\frac{9}{4}})^{2015}}$.
分析 先求出正方形ABCD的边长和面积,再求出第一个正方形A1B1C1C的面积,得出规律,根据规律即可求出正方形A2015B2015C2015C2014的面积.
解答 解:∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,
∵∠AOD=90°,
∴AB=AD=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,S正方形ABCD=($\sqrt{5}$)2=5,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴$\frac{B{A}_{1}}{OA}=\frac{AB}{OD}$,即$\frac{B{A}_{1}}{1}=\frac{\sqrt{5}}{2}$,
∴BA1=$\frac{\sqrt{5}}{2}$,
∴CA1=$\frac{3\sqrt{5}}{2}$,
∴正方形A1B1C1C的面积=($\frac{3\sqrt{5}}{2}$)2=5×$\frac{9}{4}$=$\frac{45}{4}$,…,第n个正方形的面积为5×($\frac{9}{4}$)n,
∴第2015个正方形即A2015B2015C2015C2014的面积为5×($\frac{9}{4}$)2015;
故答案为:5,$\frac{45}{4}$,5×${({\frac{9}{4}})^{2015}}$.
点评 本题考查了正方形的性质以及坐标与图形性质;通过求出正方形ABCD和正方形A1B1C1C的面积得出规律是解决问题的关键.

练习册系列答案
相关题目
9.已知:$\frac{x+y}{x-2y}=\frac{5}{2}$,则$\frac{x}{y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | 3 | D. | 4 |
19.若抛物线y=x2-4x+4-t(t为实数)在0<x<3的范围内与x轴有公共点,则t的取值范围为( )
| A. | 0<t<4 | B. | 0≤t<4 | C. | 0<t<1 | D. | t≥0 |
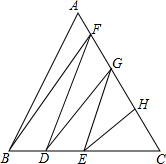 如图所示,等边三角形ABC的边长是100cm,用折线把这个等边三角形分割成面积相等的六个三角形,那么图中CD+CG的长是多少?
如图所示,等边三角形ABC的边长是100cm,用折线把这个等边三角形分割成面积相等的六个三角形,那么图中CD+CG的长是多少?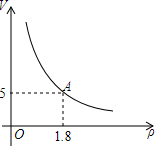 如图,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,求:
如图,一定质量的氧气,其体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图,求: