题目内容
13.若抛物线y=x2-2x-k与x轴有两个交点,则实数k的取值范围是k>-1.分析 抛物线y=x2-2x-k与x轴有两个交点,则△≥0,从而可求得k的取值范围.
解答 解:∵抛物线y=x2-2x-k与x轴有两个交点,
∴△>0,即(-2)2-4×1×(-k)>0.
整理得:4+4k>0.
解得:k>-1.
故答案为:k>-1.
点评 本题主要考查的是抛物线与x轴的交点,明确当△>0是抛物线与x轴有两个交点是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
4.若-6xayzb与9x3ycz2是同类项,则a、b、c的值分别是( )
| A. | a=1,b=2,c=3 | B. | a=3,b=1,c=2 | C. | a=3,b=2,c=1 | D. | 以上都不对 |
8.已知两个相似三角形的相似比为2:3,那么这两个三角形的面积之比为( )
| A. | 3:2 | B. | 4:6 | C. | 4:9 | D. | 2:3 |
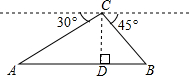 如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米.
如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米. 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.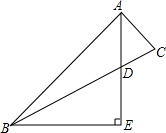 已知:如图,在△ABC中,AB=3AC,AD平分∠BAC,BE⊥AD交AD的延长线于点E.设△ACD的面积是S.
已知:如图,在△ABC中,AB=3AC,AD平分∠BAC,BE⊥AD交AD的延长线于点E.设△ACD的面积是S.