0 265914 265922 265928 265932 265938 265940 265944 265950 265952 265958 265964 265968 265970 265974 265980 265982 265988 265992 265994 265998 266000 266004 266006 266008 266009 266010 266012 266013 266014 266016 266018 266022 266024 266028 266030 266034 266040 266042 266048 266052 266054 266058 266064 266070 266072 266078 266082 266084 266090 266094 266100 266108 366461

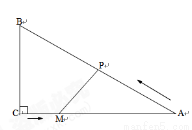
 (cm),求y与t之间的函数关系式;
(cm),求y与t之间的函数关系式; ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由;