题目内容
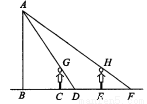
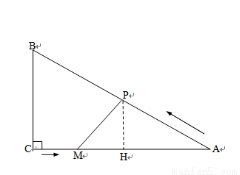
(本小题满分12分) 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
(1)当AP=AM时,求t的值.
(2)设四边形BPMC的面积为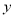 (cm),求y与t之间的函数关系式;
(cm),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的 ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由;
(4)是否存在某一时刻t,使以M,P,A为顶点的三角形与△ABC相似?若存在,求出相应t的值;若不存在,说明理由.
(1)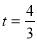 ;(2)y =
;(2)y =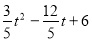 ;(3)t=2;(4)
;(3)t=2;(4)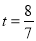 或
或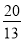 .
.
【解析】
试题分析:(1)因为AM=4-t,AP=2t,所以当AP=AM时,则4-t= 2t,解方程得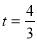 ;(2)过点P作PH⊥AC于点H,根据
;(2)过点P作PH⊥AC于点H,根据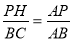 得PH=
得PH=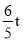 ,利用
,利用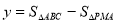 可求出函数关系式y =
可求出函数关系式y =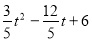 ;(3)假设存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的
;(3)假设存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的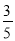 ,则
,则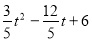 =
=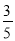 ×6,然后解方程即可;(4)分△AMP∽△ABC和△APM∽△ABC两种情况讨论.
×6,然后解方程即可;(4)分△AMP∽△ABC和△APM∽△ABC两种情况讨论.
试题解析:【解析】
(1)如图,
∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得AB=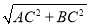 =5cm.
=5cm.
AM=4-t,AP=2t
当AP=AM时,则
4-t= 2t, ∴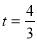
当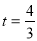 时, AP=AM 3分
时, AP=AM 3分
过点P作PH⊥AC于点H,则PH∥BC,
∴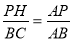 ,即
,即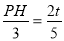 ∴PH=
∴PH=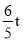 .
.
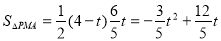
∴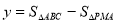 =6-(
=6-(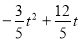 )
)
y =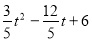 7分
7分
(3)假设存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的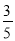 ,则
,则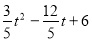 =
=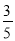 ×6,解方程得
×6,解方程得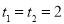 ,因为(0<t<2.5),所以当t=2时,四边形BPMC的面积是Rt△ABC面积的
,因为(0<t<2.5),所以当t=2时,四边形BPMC的面积是Rt△ABC面积的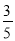 ; 9分
; 9分
(4)分两种情况讨论,当 △AMP∽△ABC时 所以
所以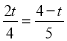 解得
解得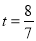 ,当△APM∽△ABC时,
,当△APM∽△ABC时,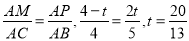 ,所以当
,所以当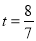 或
或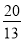 时,以M,P,A为顶点的三角形与△ABC相似 12分.
时,以M,P,A为顶点的三角形与△ABC相似 12分.
考点:1.勾股定理;2.等腰三角形的性质;3.相似三角形的判定与性质;4.函数与几何知识.

 高效智能课时作业系列答案
高效智能课时作业系列答案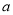 -1)x
-1)x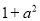 =1是一元二次方程,则
=1是一元二次方程,则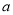 的值是( )
的值是( )
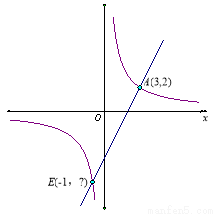
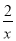 (x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
(x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2( ,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(
,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(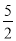 ,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .
,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .