题目内容
(本小题满分8分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
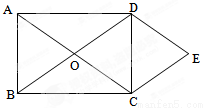
(1)判断四边形OCED的形状,并进行证明;
(2)点E是否在AB的垂直平分线上?若在,请进行证明;若不在,请说明理由.
(1)菱形,证明见解析;(2)点E在AB的垂直平分线上.
【解析】
试题分析:(1)观察图形可猜测:四边形OCED为菱形,先证明四边形DOCE是平行四边形,然后再证明有一组领边相等即可;(2)连接AE,BE,通过证△ADE≌△BCE得出 AE=BE即可.
试题解析:证明:(1)证明:∵DE∥AC,CE∥BD,
∴四边形DOCE是平行四边形,
∵矩形ABCD的对角线AC、BD相交于点O,
∴AO=CO=DO=BO,
∴平行四边形OCED为菱形; 4分
(2)【解析】
AE=BE. 5分
理由:连接AE,BE
∵四边形OCED为菱形,
∴ED=CE,∴∠EDC=∠ECD,
∴∠ADE=∠BCE,
在△ADE和△BCE中,

∴△ADE≌△BCE(SAS),
∴AE=BE.
∴点E在AB的垂直平分线上 8分
考点:1.矩形的性质;2. 菱形的判定;3.全等三角形的判定与性质;4.线段的垂直平分线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 甲_____
甲_____ _____s
_____s ;
;
 根的情况.
根的情况.  与x轴的两个交点坐标.
与x轴的两个交点坐标.
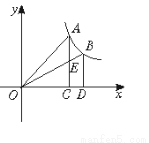
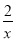 (x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小: .
(x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小: .