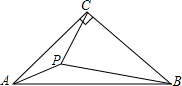
 如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )
如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )| A、105° | B、120° |
| C、135° | D、150° |
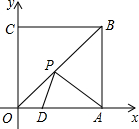 如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )
如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )| A、AC | B、BD | C、CD | D、不确定 |
 如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )
如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )| A、105° | B、120° |
| C、135° | D、150° |
 如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )
如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )| A、AC | B、BD | C、CD | D、不确定 |