题目内容
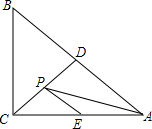 如图,等腰直角△ABC中,∠ACB=90°,AB=2
如图,等腰直角△ABC中,∠ACB=90°,AB=2| 2 |
考点:轴对称-最短路线问题
专题:
分析:过E作关于直线CD的对称点E′,连接AE′,由轴对称的性质可知AE′即为PA+PE的最小值,再由勾股定理求得PA+PE的最小值,即可求得△AEP周长的最小值.
解答: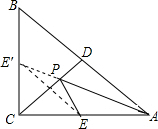 解:如图,过E作关于直线CD的对称点E′,连接AE′,由轴对称的性质可知AE′即为PA+PE的最小值,PA+PB的最小值=AE′,
解:如图,过E作关于直线CD的对称点E′,连接AE′,由轴对称的性质可知AE′即为PA+PE的最小值,PA+PB的最小值=AE′,
∵等腰直角△ABC中,∠ACB=90°,AB=2
cm,CE=1cm,
∴BC=AC=2cm,
∴AE=2═-1=1cm,
∵CD是AB的中线,
∴CD⊥AB,∠BCD=∠ACD=45°,
由对称性,CE=CE′=1cm,
∴AE′=
=
=
cm,
即PA+PE的最小值=
cm,
∴△AEP周长的最小值=
+1.
故答案为
+1.
 解:如图,过E作关于直线CD的对称点E′,连接AE′,由轴对称的性质可知AE′即为PA+PE的最小值,PA+PB的最小值=AE′,
解:如图,过E作关于直线CD的对称点E′,连接AE′,由轴对称的性质可知AE′即为PA+PE的最小值,PA+PB的最小值=AE′,∵等腰直角△ABC中,∠ACB=90°,AB=2
| 2 |
∴BC=AC=2cm,
∴AE=2═-1=1cm,
∵CD是AB的中线,
∴CD⊥AB,∠BCD=∠ACD=45°,
由对称性,CE=CE′=1cm,
∴AE′=
| AC2+CE′2 |
| 22+12 |
| 5 |
即PA+PE的最小值=
| 5 |
∴△AEP周长的最小值=
| 5 |
故答案为
| 5 |
点评:本题考查的是轴对称-最短路线问题,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知ax|a|-1+8=2(x-2)是关于x的一元一次方程,则( )
| A、a≠2 | B、a=±1或-2 |
| C、a=±1 | D、a=-2 |
 如图,在直角坐标系中,点P为菱形OACB的对角线AB、OC的交点,其中点B、P在双曲线y=
如图,在直角坐标系中,点P为菱形OACB的对角线AB、OC的交点,其中点B、P在双曲线y=| k |
| x |
A、(-1,
| ||||
B、(-2,
| ||||
C、(-
| ||||
D、(-3,
|
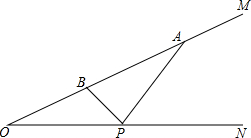 如图,已知∠MON=30°,在OM上有两点A、B分别到ON的距离为2cm和1cm,若在ON上找一点P使|PA-PB|的值最大,求P点到O点的距离.
如图,已知∠MON=30°,在OM上有两点A、B分别到ON的距离为2cm和1cm,若在ON上找一点P使|PA-PB|的值最大,求P点到O点的距离.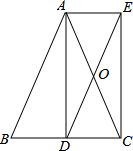 如图,在△ABC中,AB=AC,点D是BC的中点,作AE∥BC,CE∥AD,AE、CE交于点E.
如图,在△ABC中,AB=AC,点D是BC的中点,作AE∥BC,CE∥AD,AE、CE交于点E.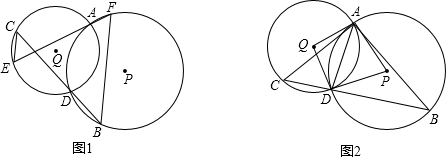
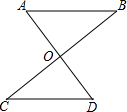 已知:如图,AD与BC相交于点O,OA=OD,OB=OC.求证:
已知:如图,AD与BC相交于点O,OA=OD,OB=OC.求证: