题目内容
 已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若
已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若| 1 |
| CE |
| 1 |
| BF |
| 1 |
| a |
考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:作辅助线构造两对相似三角形,借助等边三角形的性质分别求出
、
关于边长m的代数式,问题即可解决.
| 1 |
| CE |
| 1 |
| BF |
解答:解:过点D分别作DP∥AB,DQ∥AC,交BC于点P、Q;
∵点M、N分别为AB、AC边的中点,
∴MN∥BC,MN=
BC;
∴四边形DMBP、四边形DNCQ分别是平行四边形,
∴BP=DM,CQ=DN,
∴BP+CQ=MN=
BC,PQ=BC-
BC=
BC(设为m)
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°;
而∠DPQ=∠ABC=60°,∠DQP=∠ACB=60°,
∴△DPQ是等边三角形,DP=DQ=PQ=
m;
∵DQ∥AC,
∴
=
,
=
=
;
同理可证:
=
;
∴
+
=
,
而BQ+CP=(BQ+CQ)+PQ=m+
m=
m,
∴
+
=
;
又∵
+
=
,
∴
=
,m=3a;
即△ABC的边长为3a.
∵点M、N分别为AB、AC边的中点,
∴MN∥BC,MN=
| 1 |
| 2 |
∴四边形DMBP、四边形DNCQ分别是平行四边形,
∴BP=DM,CQ=DN,
∴BP+CQ=MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°;
而∠DPQ=∠ABC=60°,∠DQP=∠ACB=60°,
∴△DPQ是等边三角形,DP=DQ=PQ=
| 1 |
| 2 |
∵DQ∥AC,
∴
| DQ |
| CE |
| BQ |
| BC |
| 1 |
| CE |
| BQ |
| DQ•BC |
| 2BQ |
| m2 |
同理可证:
| 1 |
| BF |
| 2CP |
| m2 |
∴
| 1 |
| CE |
| 1 |
| BF |
| 2(BQ+CP) |
| m2 |
而BQ+CP=(BQ+CQ)+PQ=m+
| 1 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| CE |
| 1 |
| BF |
| 3 |
| m |
又∵
| 1 |
| CE |
| 1 |
| BF |
| 1 |
| a |
∴
| 3 |
| m |
| 1 |
| a |
即△ABC的边长为3a.
点评:该题考查了等边三角形的性质、相似三角形的判定及其性质的应用问题;解题的关键是通过作辅助线构造相似三角形;对综合运用能力提出了较高的要求.

练习册系列答案
相关题目
直线a、b、c是三条平行直线.已知a与b的距离为7cm,b与c的距离为3cm,则a与c的距离为( )
| A、4cm | B、10cm |
| C、3cm | D、4cm或10cm |
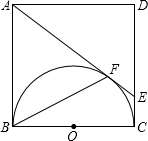 如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A点作半圆的切线,与半圆相切于点F,与DC相交于点E,求BF的长.
如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A点作半圆的切线,与半圆相切于点F,与DC相交于点E,求BF的长. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.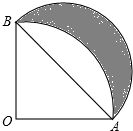 已知扇形AOB的半径为R,∠AOB=90°,以弦AB为直径作半圆,得到如图图形.你会求图中“新月形”(阴影部分)的面积吗?
已知扇形AOB的半径为R,∠AOB=90°,以弦AB为直径作半圆,得到如图图形.你会求图中“新月形”(阴影部分)的面积吗? 如图,CD、BE相交于点A,若∠B=66°,∠DAE=67°,则∠C=
如图,CD、BE相交于点A,若∠B=66°,∠DAE=67°,则∠C=