题目内容
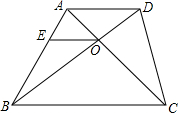 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,(1)求△BOC和△DOC的面积;
(2)求OE的长.
考点:相似三角形的判定与性质,梯形
专题:
分析:(1)根据平行的相似,推出
=
=
=
=
,求出
=(
)2,
=
=
即可;
(2)根据平行得出相似,推出
=
=
,代入求出即可.
| OA |
| OC |
| OD |
| OB |
| AD |
| BC |
| 6cm |
| 12cm |
| 1 |
| 2 |
| S△AOD |
| S△BOC |
| 1 |
| 2 |
| S△AOD |
| S△DOC |
| AO |
| OC |
| 1 |
| 2 |
(2)根据平行得出相似,推出
| OE |
| AD |
| BO |
| BD |
| 2 |
| 3 |
解答:解:(1)∵AD∥BC,
∴△AOD∽△COB,
∴
=
=
=
=
,
∴
=(
)2,
=
=
,
∵△AOD的面积为6cm2,
∴△DOC的面积为2S△AOD=12cm2,△BOC的面积为4S△AOD=24cm2;
(2)∵OE∥AD,
∴△BEO∽△BAD,
∴
=
=
=
,
∵AD=6cm,
∴OE=4cm.
∴△AOD∽△COB,
∴
| OA |
| OC |
| OD |
| OB |
| AD |
| BC |
| 6cm |
| 12cm |
| 1 |
| 2 |
∴
| S△AOD |
| S△BOC |
| 1 |
| 2 |
| S△AOD |
| S△DOC |
| AO |
| OC |
| 1 |
| 2 |
∵△AOD的面积为6cm2,
∴△DOC的面积为2S△AOD=12cm2,△BOC的面积为4S△AOD=24cm2;
(2)∵OE∥AD,
∴△BEO∽△BAD,
∴
| OE |
| AD |
| BO |
| BD |
| 2 |
| 2+1 |
| 2 |
| 3 |
∵AD=6cm,
∴OE=4cm.
点评:本题考查了相似三角形的性质和判定,三角形的面积的应用,注意:相似三角形的面积比等于相似比的平方,题目比较好,难度适中.

练习册系列答案
相关题目
化简
-(
+2)÷
得( )
| 8 |
| 2 |
| 2 |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
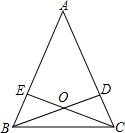 如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )
如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )| A、都正确 |
| B、都不正确 |
| C、只有一个正确 |
| D、只有一个不正确 |
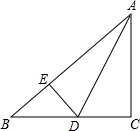 如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )
如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )| A、∠ADE=∠ADC |
| B、∠BAC=∠BDE |
| C、DC=DE |
| D、∠ADE=∠BDE |
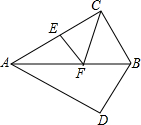 两个全等的含30°的直角三角板如图放置(斜边重合),点E是AC的中点,AC=2,若点F是直线AB上的一个动点,则△CEF的周长最小值是
两个全等的含30°的直角三角板如图放置(斜边重合),点E是AC的中点,AC=2,若点F是直线AB上的一个动点,则△CEF的周长最小值是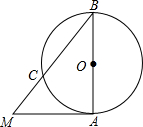 已知:在⊙O中,AB是直径,AM与⊙O相切于点A,连接BM交⊙O于点C,若AM=6,半径为4,求BC的长.
已知:在⊙O中,AB是直径,AM与⊙O相切于点A,连接BM交⊙O于点C,若AM=6,半径为4,求BC的长.