题目内容
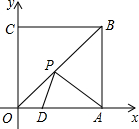如图所示，四边形OABC为正方形，点A，C分别在x轴，y轴的正半轴上，点D在OA上，在OB上求作一点P，使得PD+PA的值最小，则可连接（ ）| A、AC | B、BD | C、CD | D、不确定 |
考点：轴对称-最短路线问题,坐标与图形性质
专题：
分析：根据两点之间线段最短，所以P是连接A的对称点和D点的线段与OB的交点，由轴对称的性质可知CD即为PD+PA的最小值．
解答：解：∵四边形OABC为正方形，
∴C是A点关于对角线BC的对称点，
∴连接CD交CB于P，此时PD+PA的值最小，
∴在OB上求作一点P，使得PD+PA的值最小，则可连接CD．
故选C．
∴C是A点关于对角线BC的对称点，
∴连接CD交CB于P，此时PD+PA的值最小，
∴在OB上求作一点P，使得PD+PA的值最小，则可连接CD．
故选C．
点评：本题考查了轴对称-最短路线问题，找出A的对称点是本题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
下列命题中，不正确是（ ）
| A、若a＞2，则a-2＞0 |
| B、若a＞2，则2-a＜0 |
| C、若ac2＞bc2，则a＞b |
| D、若a＞b，则ac2＞bc2 |
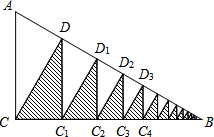如图，已知Rt△ABC中，∠B=30°，AC=2，作△CDB的高DC1，作△DC1B的高C1D1，…，就这样无限作下去，求图中阴影部分的面积．
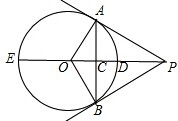如图，PA、PB是⊙O的两条切线，点A、B为切点，直线OP交⊙O于点D、E，交AB于点C．