题目内容
 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.考点:轴对称-最短路线问题,勾股定理,垂径定理
专题:
分析:过B作关于直线MN的对称点B′,连接AB′,由轴对称的性质可知AB′即为PA+PB的最小值,由同弧所对的圆心角和圆周角的性质可知∠AON=2∠AMN=2×30°=60°,由对称的性质可知∠B′ON=∠BON=30°,即可求出∠AOB′的度数,再由勾股定理即可求解.
解答: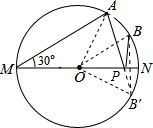 解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,
解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,
则AB′与MN的交点即为PA+PB的最小时的点,PA+PB的最小值=AB′,
∵∠AMN=30°,
∴∠AON=2∠AMN=2×30°=60°,
∵点B为劣弧AN的中点,
∴∠BON=∠AON=
×60°=30°,
由对称性,∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,
∴△AOB′是等腰直角三角形,
∴AB′=
OA=
×1=
,
即PA+PB的最小值=
.
 解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,
解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,则AB′与MN的交点即为PA+PB的最小时的点,PA+PB的最小值=AB′,
∵∠AMN=30°,
∴∠AON=2∠AMN=2×30°=60°,
∵点B为劣弧AN的中点,
∴∠BON=∠AON=
| 1 |
| 2 |
由对称性,∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,
∴△AOB′是等腰直角三角形,
∴AB′=
| 2 |
| 2 |
| 2 |
即PA+PB的最小值=
| 2 |
点评:本题考查的是圆周角定理及勾股定理,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算-(-3)2的结果是( )
| A、6 | B、-6 | C、9 | D、-9 |
 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为( )
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为( )| A、8 | B、16 | C、32 | D、64 |
适合关系式|x+
|+|x-
|=2的整数解x的个数是( )
| 2 |
| 3 |
| 4 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若
已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若 如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题: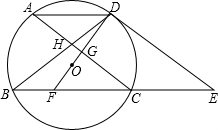 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.