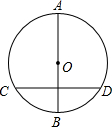
如图.在⊙O中AB为直径.CD为非直径的弦.AB平分CD,(3)AB平分CD所对的两条弧．若以中的一个为条件.另两个为结论构成三个命题.其中真命题的个数为( ) A.3B.2C.1D——青夏教育精英家教网——

如图，在⊙O中AB为直径，CD为非直径的弦，（1）AB⊥CD；（2）AB平分CD；（3）AB平分CD所对的两条弧．若以（1）、（2）、（3）中的一个为条件，另两个为结论构成三个命题，其中真命题的个数为（　　）

已知圆外切正六边形周长为4

cm，求圆内接正方形的边长．

如图，四边形ABCD，EFGH分别是⊙O的外切正四边形和内接正四边形，则

等于（　　）

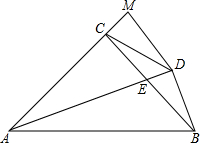如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD，且CD=BD．下列结论：
①AC+CE=AB；②CD=

AE；③∠CDA=45°；④AC+AB=2AM．
其中正确的结论有（　　）

如图，在四边形ABCD中，AB=DC，∠ABC=∠DCB，点E、F分别在AB、BC上，且BE=2AE，CF=2DF．求证：∠BEC=∠CFB．

如图1，O是正△ABC的内心，分别延长OA、OC到点E、D，使OE=2OA，OD=2OC，连接DE，将△DOE绕点O逆时针旋转α角得到△D₁OE₁（如图2所示）．
（1）猜想AE₁和CD₁之间的数量关系，并给予证明；
（2）当α=60°时，求证：OD₁⊥AC．

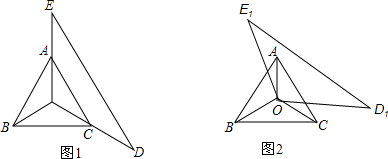
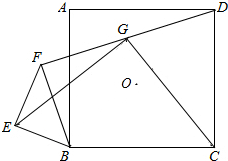正方形ABCD中，以B为端点在正方形外作等腰直角△BEF，∠BEF=90°，连接DF，取DF的中点G，并连接EG、CG．求证：EG=CG，EG⊥CG．

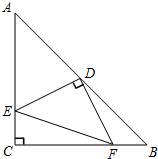如图，在Rt△ABC中，AC=BC，∠ACB=90°，D为AB边的中点，∠EDF=90°，它的两边分别交AC、BC于点E、F，当DE⊥AC时，试判断△EDF的具体形状．

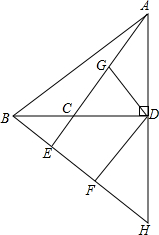已知，如图，在钝角△ABC中，BE和AD分别是AC和BC边上的高，BE和AD的延长线交于点H，点F、G分别是BH、AC的中点．
（1）求证：∠FDG=90°；
（2）联结FG，试问△FDG能否为等腰直角三角形？若能，试求∠ABC的度数，并写出推理过程；若不能，请简要说明理由．

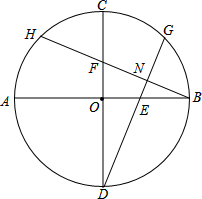在⊙O中，已知直径AB与直径CD垂直于O，E在OB上，F在OC，且OE=OF，连接DE且延长交⊙O于G，连接BF且延长交⊙O于H，BH与DG相交于N．求证：BH⊥GD．

0 250967 250975 250981 250985 250991 250993 250997 251003 251005 251011 251017 251021 251023 251027 251033 251035 251041 251045 251047 251051 251053 251057 251059 251061 251062 251063 251065 251066 251067 251069 251071 251075 251077 251081 251083 251087 251093 251095 251101 251105 251107 251111 251117 251123 251125 251131 251135 251137 251143 251147 251153 251161 366461