题目内容
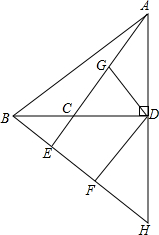 已知,如图,在钝角△ABC中,BE和AD分别是AC和BC边上的高,BE和AD的延长线交于点H,点F、G分别是BH、AC的中点.
已知,如图,在钝角△ABC中,BE和AD分别是AC和BC边上的高,BE和AD的延长线交于点H,点F、G分别是BH、AC的中点.(1)求证:∠FDG=90°;
(2)联结FG,试问△FDG能否为等腰直角三角形?若能,试求∠ABC的度数,并写出推理过程;若不能,请简要说明理由.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证∠GDC=∠ECB和∠FBD=∠FDB,根据Rt△BEC中∠EBC+∠ECB=90°即可解题;
(2)△FDG能为等腰直角三角形.理由:连接FG,若DG=DF,则BH=AC,易证∠EAH=∠DBH,即可证明△BDH≌△ADC,可得BD=AD,根据∠BDA=90°,即可解题.
(2)△FDG能为等腰直角三角形.理由:连接FG,若DG=DF,则BH=AC,易证∠EAH=∠DBH,即可证明△BDH≌△ADC,可得BD=AD,根据∠BDA=90°,即可解题.
解答:解:(1)∵在Rt△ADC中,GA=GC,
∴DG=GC,
∴∠GCD=∠GDC,
又∵∠ECB=∠GCD,
∴∠GDC=∠ECB;
同理∠FBD=∠FDB,
∵在Rt△BEC中,∠EBC+∠ECB=90°,
∴∠GDC+∠FDB=90°,即∠FDG=90°
(2)△FDG能为等腰直角三角形.
理由:连接FG,
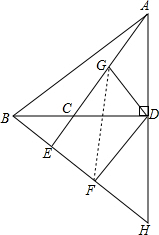
若DG=DF,而DG=
AC,DF=
BH,
∴BH=AC,
∵∠EAH+∠BHD=90°,∠BHD+∠DBH=90°,
∴∠EAH=∠DBH,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠BDA=90°,
∴∠ABC=45°.
∴DG=GC,
∴∠GCD=∠GDC,
又∵∠ECB=∠GCD,
∴∠GDC=∠ECB;
同理∠FBD=∠FDB,
∵在Rt△BEC中,∠EBC+∠ECB=90°,
∴∠GDC+∠FDB=90°,即∠FDG=90°
(2)△FDG能为等腰直角三角形.
理由:连接FG,

若DG=DF,而DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴BH=AC,
∵∠EAH+∠BHD=90°,∠BHD+∠DBH=90°,
∴∠EAH=∠DBH,
在△BDH和△ADC中,
|
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠BDA=90°,
∴∠ABC=45°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BDH≌△ADC是解题的关键.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、平行四边形的对边相等 |
| B、菱形的四条边相等 |
| C、矩形的对边平行且相等 |
| D、平行四边形的对角线相等 |
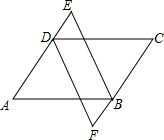 如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF.
如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF.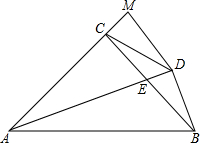 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,且CD=BD.下列结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,且CD=BD.下列结论: 如图,数轴上的A,B,C三点所表示的数分别是a,b,c,其中AB=BC,若|a|>|b|>|c|,则该数轴的原点O的位置应该在
如图,数轴上的A,B,C三点所表示的数分别是a,b,c,其中AB=BC,若|a|>|b|>|c|,则该数轴的原点O的位置应该在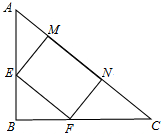 如图,在Rt△ABC中,AC=40,BC=30,在其内部挖出一个矩形,问挖出的矩形的最大面积是多少?
如图,在Rt△ABC中,AC=40,BC=30,在其内部挖出一个矩形,问挖出的矩形的最大面积是多少?