Question

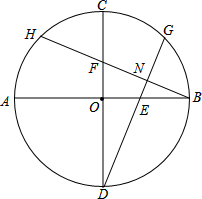在⊙O中，已知直径AB与直径CD垂直于O，E在OB上，F在OC，且OE=OF，连接DE且延长交⊙O于G，连接BF且延长交⊙O于H，BH与DG相交于N．求证：BH⊥GD．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：求出△BOF≌△DOE，根据全等三角形的性质得出∠FBO=∠ODE，求出∠ENB=90°即可．

解答：证明：∵CD⊥AB，
∴∠FOB=∠EOD=90°，
在△BOF和△DOE中，

OB=OD ∠FOB=∠EOD OF=OE

，
∴△BOF≌△DOE（SAS），
∴∠FBO=∠ODE，
∵∠EOD=90°，
∴∠ODE+∠OED=90°，
∵∠OED=∠NEB，
∴∠FBO+∠NEB=90°，
∴∠ENB=90°，
∴BH⊥DG．

点评：本题考查了垂直定义，全等三角形的性质和判定的应用，解此题的关键是推出∠ODE=∠FBO，题目比较好，难度适中．