题目内容
 如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则
如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则| EF |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正多边形和圆
专题:
分析:如图,作辅助线,首先求出⊙O的外切正方形的边长(用半径λ表示);再次求出⊙O的内接正方形的边长,问题即可解决.
解答: 解:如图,连接OB、OC、ON;
解:如图,连接OB、OC、ON;
则OB=OC,ON⊥BC;∠BOC=90°;
故∠BON=∠CON=45°,而∠OBN=45°,
∴∠OBN=∠BON,BN=ON=λ(λ为⊙O的半径);
同理可证CN=ON=λ;
∴BC=2λ;连接OE、OF;
则∠EOF=90°;由勾股定理得:
EF2=λ2+λ2=2λ2,
∴EF=
λ;
∴
=
=
,
故选C.
 解:如图,连接OB、OC、ON;
解:如图,连接OB、OC、ON;则OB=OC,ON⊥BC;∠BOC=90°;
故∠BON=∠CON=45°,而∠OBN=45°,
∴∠OBN=∠BON,BN=ON=λ(λ为⊙O的半径);
同理可证CN=ON=λ;
∴BC=2λ;连接OE、OF;
则∠EOF=90°;由勾股定理得:
EF2=λ2+λ2=2λ2,
∴EF=
| 2 |
∴
| EF |
| AB |
| ||
| 2λ |
| ||
| 2 |
故选C.
点评:该题主要考查了正多边形和圆的位置关系及其性质的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断;对求解计算能力提出了一定的要求.

练习册系列答案
相关题目
在3.14,
,0,
,
,0.150250015…中,无理数有( )
| 13 |
| 3 | 8 |
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,AC=AB,∠BAC=90°,D是BC上的一动点,过点C作CE⊥BC,连接DE,求证:∠BAD=∠EDC.
如图,在△ABC中,AC=AB,∠BAC=90°,D是BC上的一动点,过点C作CE⊥BC,连接DE,求证:∠BAD=∠EDC.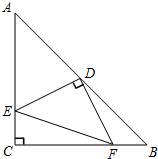 如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,∠EDF=90°,它的两边分别交AC、BC于点E、F,当DE⊥AC时,试判断△EDF的具体形状.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,∠EDF=90°,它的两边分别交AC、BC于点E、F,当DE⊥AC时,试判断△EDF的具体形状. 阅读下面材料并回答问题:
阅读下面材料并回答问题: 如图所示,半径为1的圆O内切于一个圆心角为60°的扇形,圆O与扇形的半径和圆弧分别相切于点A,B,扇形所在的圆心为C,连接CB,求扇形的弧长.
如图所示,半径为1的圆O内切于一个圆心角为60°的扇形,圆O与扇形的半径和圆弧分别相切于点A,B,扇形所在的圆心为C,连接CB,求扇形的弧长. 如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.
如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.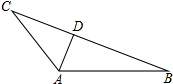 如图,
如图,