题目内容
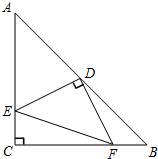 如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,∠EDF=90°,它的两边分别交AC、BC于点E、F,当DE⊥AC时,试判断△EDF的具体形状.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,∠EDF=90°,它的两边分别交AC、BC于点E、F,当DE⊥AC时,试判断△EDF的具体形状.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:连接CD,易证∠CDE=∠BDF,即可证明△CDE≌△BDF,可得DE=DF,即可解题.
解答:解:连接CD,
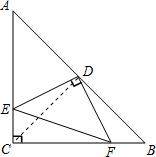
∵AC=BC,∠ACB=90°,D为AB边的中点,
∴CD=AD=BD,∠ECD=∠B=45°,
∵∠CDE+∠CDF=90°,∠BDF+∠CDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中,
,
∴△CDE≌△BDF(ASA),
∴DE=DF,
∴△EDF是等腰直角三角形.

∵AC=BC,∠ACB=90°,D为AB边的中点,
∴CD=AD=BD,∠ECD=∠B=45°,
∵∠CDE+∠CDF=90°,∠BDF+∠CDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中,
|
∴△CDE≌△BDF(ASA),
∴DE=DF,
∴△EDF是等腰直角三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CDE≌△BDF是解题的关键.

练习册系列答案
相关题目
下列命题是真命题的是( )
| A、4是2的平方根 |
| B、2是4的算术平方根 |
| C、0的算术平方根不存在 |
| D、-1是-1的算术平方根 |
 如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则
如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则| EF |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列四个函数中,y随x的增大而减小的是( )
| A、y=3x | ||
| B、y=x2(x<0) | ||
| C、y=x+3 | ||
D、y=
|
下列命题是真命题的是( )
| A、等底等高的两个三角形全等 |
| B、周长相等的直角三角形都全等 |
| C、有两边和一角对应相等的两个三角形全等 |
| D、有一边对应相等的两个等边三角形全等 |
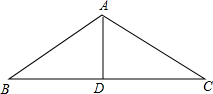 如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.
如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数. 如图,已知点C为BD的中点,AB∥DE,∠1=∠2.求证:AF=EG.
如图,已知点C为BD的中点,AB∥DE,∠1=∠2.求证:AF=EG.