下列函数图象与x轴有两个交点的是( )
| A、y=7(x+8)2+2 |
| B、y=7(x-8)2+2 |
| C、y=-7(x-8)2-2 |
| D、y=-7(x+8)2+2 |
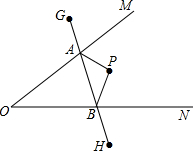 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )| A、5cm | B、10cm |
| C、20cm | D、15cm |
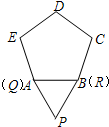 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )A、
| ||
B、
| ||
| C、8π | ||
| D、16π |
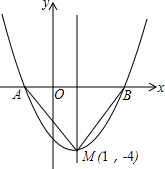 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4) 如图,AB=AC=9cm,BC=4cm,点A和点B关于直线l对称,AC与直线l相交于点D,则△BDC的周长是
如图,AB=AC=9cm,BC=4cm,点A和点B关于直线l对称,AC与直线l相交于点D,则△BDC的周长是 如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB∥CD;④AO=OC.其中正确的结论有
如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB∥CD;④AO=OC.其中正确的结论有 如图,已知A(-4,n)、B(2,-4)是一次函数y=k1x+b1的图象和反比例函数y=
如图,已知A(-4,n)、B(2,-4)是一次函数y=k1x+b1的图象和反比例函数y=