题目内容
19.学校举行数学选拔赛,共举行4次,肖明、李光、章红、孙望4名同学每次都名列前茅,各次的成绩如表(单位:分).| 肖明 | 李光 | 章红 | 孙望 | |
| 第1次 | 92 | 95 | 84 | 81 |
| 第2次 | 88 | 89 | 96 | 92 |
| 第3次 | 92 | 90 | 98 | 98 |
| 第4次 | 96 | 94 | 90 | 97 |
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
分析 (1)根据平均数和方差的计算公式列式计算即可;
(2)根据4名同学这4次比赛成绩的平均数和方差的结果,在平均数相同的情况下,选出方差较小的即可.
解答 解:(1)$\overline{{x}_{肖明}}$=$\frac{1}{4}$(92+88+92+96)=92(分),
$\overline{{x}_{李光}}$=$\frac{1}{4}$(95+89+90+94)=92(分),
$\overline{{x}_{章红}}$=$\frac{1}{4}$(84+96+98+90)=92(分),
$\overline{{x}_{孙望}}$=$\frac{1}{4}$(81+92+98+97)=92(分);
S肖明2=$\frac{1}{4}$[(92-92)2+(88-92)2+(92-92)2+(96-92)2]=8,
S李光2=$\frac{1}{4}$[(95-92)2+(89-92)2+(90-92)2+(94-92)2]=6.5,
S章红2=$\frac{1}{4}$[(84-92)2+(96-92)2+(98-92)2+(90-92)2]=30,
S孙望2=$\frac{1}{4}$[(81-92)2+(92-92)2+(98-92)2+(97-92)2]=45.5,
(2)4名同学比赛的平均数相同,说明4名同学的实力大体相当;
从方差来看,肖明与李光的方差较小,说明肖明与李光的比赛成绩更稳定,因此派肖明与李光两名同学参赛更能取得好成绩.
点评 此题考查了平均数和方差:一般地,设n个数据x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

 名校课堂系列答案
名校课堂系列答案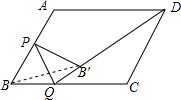 如图,菱形ABCD的边长为4,∠ABC=60°,点P是边AB的中点,点Q为边BC上的动点,联结PQ,作B关于PQ的对称点B′,则B′D长度的最小值是2$\sqrt{7}$-2.
如图,菱形ABCD的边长为4,∠ABC=60°,点P是边AB的中点,点Q为边BC上的动点,联结PQ,作B关于PQ的对称点B′,则B′D长度的最小值是2$\sqrt{7}$-2. 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作⊙O的切线交AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作⊙O的切线交AC于点F. 在△ABC中,高线AD、CE交于点F,且EC=EA.
在△ABC中,高线AD、CE交于点F,且EC=EA. 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2-x与x轴交于点A,点P在抛物线上,连结AP.若△OAP是以OA为底边的等腰三角形,则△OAP的面积是$\frac{1}{2}$.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2-x与x轴交于点A,点P在抛物线上,连结AP.若△OAP是以OA为底边的等腰三角形,则△OAP的面积是$\frac{1}{2}$.