题目内容
7. 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作⊙O的切线交AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作⊙O的切线交AC于点F.(1)求证:DF⊥AC;
(2)如果sinC=$\frac{{\sqrt{3}}}{3}$,AE的长为2.求⊙O的半径.
分析 (1)连接OD.由切线的性质可知OD⊥DF.接下来由AC=AB,OB=OD可证明∠∠ODB=∠C,从而可证明OD∥AC,由平行线的性质可证明DF⊥AC;
(2)连结BE,AD.先证明FD∥BE,由平行线分线段成比例定理可知:F是CE的中点.设⊙O的半径为r,则AB=AC=2r.则CE=2r+2,AF=r-1,在△ABD中由锐角三角函数的定义可知AD=$\frac{{2\sqrt{3}}}{3}r$.最后依据sin∠ADF=$\frac{{\sqrt{3}}}{3}$列出关于r的方程求解即可.
解答 (1)证明:如图1所示:连接OD.
∵DF是⊙O的切线,
∴OD⊥DF.
∵OB=OD,
∴∠B=∠ODB.
∵AB=AC.
∴∠B=∠C.
∴∠ODB=∠C.
∴OD∥AC.
∴DF⊥AC.
(2)解:连结BE,AD.
∵AB是直径,
∴∠ADB=∠AEB=90°
∵AB=AC,
∴BD=CD.
∵DF⊥AC,
∴FD∥BE.
∴可得点F是CE的中点.
设⊙O的半径为r,则AB=AC=2r.则CE=2r+2,
∴FC=r+1.
∴AF=r-1.
∵∠ABD=∠C=∠ADF,
∴sin∠ABD=sin∠ACB=sin∠ADF=$\frac{{\sqrt{3}}}{3}$.
∴AD=$\frac{{2\sqrt{3}}}{3}r$.
∵sin∠ADF=$\frac{AF}{AD}$=$\frac{{\sqrt{3}}}{3}$=$\frac{r-1}{{\frac{{2\sqrt{3}}}{3}r}}$
∴r=3.
点评 本题主要考查的是切线的性质、等腰三角形的性质、平行线的性质、平行线分线段成比例定理、锐角三角函数的定义,用含r的式子表示出AF、AD的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.学校举行数学选拔赛,共举行4次,肖明、李光、章红、孙望4名同学每次都名列前茅,各次的成绩如表(单位:分).
(1)分别计算这4名同学成绩的平均数和方差;
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
| 肖明 | 李光 | 章红 | 孙望 | |
| 第1次 | 92 | 95 | 84 | 81 |
| 第2次 | 88 | 89 | 96 | 92 |
| 第3次 | 92 | 90 | 98 | 98 |
| 第4次 | 96 | 94 | 90 | 97 |
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
 在平行四边形ABCD中,E在DC上,若DE:EC=1:2,△FEC的面积是2,平行四边形ABCD的面积是13.
在平行四边形ABCD中,E在DC上,若DE:EC=1:2,△FEC的面积是2,平行四边形ABCD的面积是13.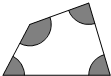 如图,已知四个扇形的半径均为1,那么图中阴影部分面积的和是π.
如图,已知四个扇形的半径均为1,那么图中阴影部分面积的和是π. 如图,在菱形ABCD中,E为BC上一点,AE交BD于F,AB=AE,BE=AF.
如图,在菱形ABCD中,E为BC上一点,AE交BD于F,AB=AE,BE=AF.