题目内容
14.已知关于x,y的方程组$\left\{\begin{array}{l}{3x-2y=2k+1}\\{x+y=k-3}\end{array}\right.$的解满足4x<y且2x>3y,(1)求k的取值范围.
(2)化简3|k+4|+|3k-2|.
分析 (1)代入法求出关于x、y的二元一次方程组,根据4x<y且2x>3y得关于k的不等式,解不等式可得;
(2)根据绝对值的性质,可得答案.
解答 解:(1)$\left\{\begin{array}{l}{3x-2y=2k+1①}\\{x+y=k-3②}\end{array}\right.$,
②×3-①得5y=k-10,y=$\frac{k-10}{5}$,
②×2+①,得5x=4k-5,x=$\frac{4k-5}{5}$,
由4x<y且2x>3y,得
$\left\{\begin{array}{l}{\frac{16k-20}{5}<\frac{k-10}{5}}\\{\frac{8k-10}{5}>\frac{3k-30}{5}}\end{array}\right.$,
解得-$\frac{2}{5}$<k<$\frac{1}{3}$;
(2)3|k+4|+|3k-2|=3k+12+2-3k=14.
点评 本题考查了二元一次方程组的解,利用方程组的解得出关于k的不等式组是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.学校举行数学选拔赛,共举行4次,肖明、李光、章红、孙望4名同学每次都名列前茅,各次的成绩如表(单位:分).
(1)分别计算这4名同学成绩的平均数和方差;
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
| 肖明 | 李光 | 章红 | 孙望 | |
| 第1次 | 92 | 95 | 84 | 81 |
| 第2次 | 88 | 89 | 96 | 92 |
| 第3次 | 92 | 90 | 98 | 98 |
| 第4次 | 96 | 94 | 90 | 97 |
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
19.下列说法正确的是( )
| A. | 若两个角互补,则一个角是锐角,一个角是钝角 | |
| B. | 有一个公共顶点的角是对顶角 | |
| C. | 若两个角互余,则这两个角一定都是锐角 | |
| D. | 两个锐角一定互为余角 |
 如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹)
如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹) 如图,在正方形ABCD中,AB=2,CA=CE,则△ACE的面积是2$\sqrt{2}$.
如图,在正方形ABCD中,AB=2,CA=CE,则△ACE的面积是2$\sqrt{2}$.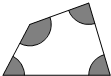 如图,已知四个扇形的半径均为1,那么图中阴影部分面积的和是π.
如图,已知四个扇形的半径均为1,那么图中阴影部分面积的和是π. 矩形DEFG的四个顶点分别在Rt△ABC的边上,∠A=90°,在Rt△DGC和Rt△BFE内又作如图所示的正方形JGHI和正方形KFML,求证:ID=EL.
矩形DEFG的四个顶点分别在Rt△ABC的边上,∠A=90°,在Rt△DGC和Rt△BFE内又作如图所示的正方形JGHI和正方形KFML,求证:ID=EL. 如图,在平行四边形ABCD中,AE、BF、CF、DE分别为∠DAB、∠ABC、∠BCD、∠CDA的平分线.
如图,在平行四边形ABCD中,AE、BF、CF、DE分别为∠DAB、∠ABC、∠BCD、∠CDA的平分线.