题目内容
9.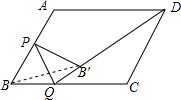 如图,菱形ABCD的边长为4,∠ABC=60°,点P是边AB的中点,点Q为边BC上的动点,联结PQ,作B关于PQ的对称点B′,则B′D长度的最小值是2$\sqrt{7}$-2.
如图,菱形ABCD的边长为4,∠ABC=60°,点P是边AB的中点,点Q为边BC上的动点,联结PQ,作B关于PQ的对称点B′,则B′D长度的最小值是2$\sqrt{7}$-2.
分析 如图,当P、B′、D共线时,B′D最小,作PM⊥DA交DA的延长线于M,先求出PM、AM,再求出PD即可解决问题.
解答 解: 如图,当P、B′、D共线时,B′D最小,作PM⊥DA交DA的延长线于M,
如图,当P、B′、D共线时,B′D最小,作PM⊥DA交DA的延长线于M,
在RT△APM中,∵∠AMP=90°,AP=2,∠MAP=60°,
∴AM=$\frac{1}{2}$AP=1,PM=$\sqrt{3}$AM=$\sqrt{3}$,
在RT△PMD中,PD=$\sqrt{P{M}^{2}+D{M}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{5}^{2}}$=2$\sqrt{7}$,
∴DB′的最小值=PD-PB′=2$\sqrt{7}$-2.
故单位2$\sqrt{7}$-2.
点评 本题考查菱形的性质、最小值问题勾股定理等知识,解题的关键是找到DB′最小时的位置,属于最小值问题中比较难的题目,记住解题的方法,寻找特殊位置取得最小值,属于中考常考题型.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
20.一元二次方程5x2-7x+5=0的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 只有一个实数根 |
19.学校举行数学选拔赛,共举行4次,肖明、李光、章红、孙望4名同学每次都名列前茅,各次的成绩如表(单位:分).
(1)分别计算这4名同学成绩的平均数和方差;
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
| 肖明 | 李光 | 章红 | 孙望 | |
| 第1次 | 92 | 95 | 84 | 81 |
| 第2次 | 88 | 89 | 96 | 92 |
| 第3次 | 92 | 90 | 98 | 98 |
| 第4次 | 96 | 94 | 90 | 97 |
(2)如果参加比赛的名额只有2个,那么应该派哪两名同学参如?说明你的理由.
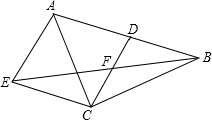 在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE
在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE 如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹)
如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹)