题目内容
18．
如图，圆O与正方形ABCD的两边AB、AD相切，且DE与圆O相切于E点．若圆O的半径为5，且AB=11，则DE=6．
分析 连接OE，OF，OG，根据AB，AD，DE都与圆O相切，利用切线的性质得到三个直角，再由半径相等，得到四边形AFOG为正方形，根据切线长定理得到DF=DE，由AD-AF求出DF的长，即为DE的长．
解答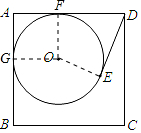 
解：连接OE，OF，OG，
∵AB，AD，DE都与圆O相切，
∴DE⊥OE，OG⊥AB，OF⊥AD，DF=DE，
∵四边形ABCD为正方形，
∴AB=AD=11，∠A=90°，
∴∠A=∠AGO=∠AFO=90°，
∵OF=OG=5，
∴四边形AFOG为正方形，
则DE=DF=11-5=6，
故答案为：6
点评 此题考查了切线的性质，以及正方形的性质，熟练掌握切线的性质是解本题的关键．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
8．
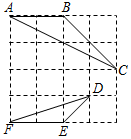如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形顶点上，则tan∠ACB的值为（ ）
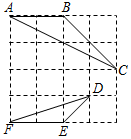如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形顶点上，则tan∠ACB的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | 3 |
6．从2开始，连续的偶数相加，它们的和的情况如下表：
（1）如果n=8时，那么S的值为72；
（2）根据表中的规律猜想：用n的代数式表示S的公式为S=2+4+6+8+…+2n=n（n+1）；
（3）由上题的规律计算100+102+104+…+2014+2016的值（要有计算过程）
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
（2）根据表中的规律猜想：用n的代数式表示S的公式为S=2+4+6+8+…+2n=n（n+1）；
（3）由上题的规律计算100+102+104+…+2014+2016的值（要有计算过程）
13．⊙O是等边△ABC的外接圆，⊙O的半径为4，则等边△ABC的边长为（ ）
| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{5}$ | C． | 4$\sqrt{3}$ | D． | 4$\sqrt{5}$ |
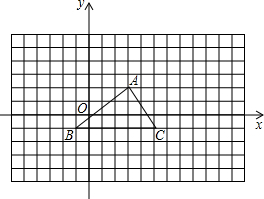如图所示的网格中，每个小方格都是边长为1的正方形，B点的坐标为（-1，-1）．
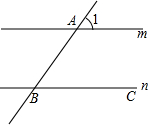如图，直线m∥n，∠1=45°，C为直线n上的一动点，且在B点右边，若△ABC为等腰三角形，则∠BAC=67.5°或45°或90°．