题目内容
8.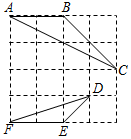 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 3 |
分析 根据勾股定理即可求出AC、BC、DE、DF的长度,然后证明△FDE∽△ABC,所以∠DFE=∠ACB,从而可知tan∠DFE=tan∠ACB=$\frac{1}{3}$,
解答 解:由勾股定理 可求出:BC=2$\sqrt{2}$,AC=2$\sqrt{5}$,DF=$\sqrt{10}$,DE=$\sqrt{2}$,
∴$\frac{FD}{AC}=\frac{\sqrt{2}}{2}$,$\frac{ED}{AB}=\frac{\sqrt{2}}{2}$,$\frac{FE}{BC}=\frac{\sqrt{2}}{2}$,
∴$\frac{FD}{AC}=\frac{ED}{AB}=\frac{FE}{BC}$,
∴△FDE∽△CAB,
∴∠DFE=∠ACB,
∴tan∠DFE=tan∠ACB=$\frac{1}{3}$,
故选(B)
点评 本题考查解直角三角形,涉及勾股定理,相似三角形的判定与性质.

练习册系列答案
相关题目
10.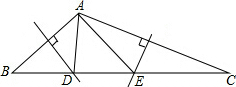 如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )
如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )
 如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )
如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )| A. | 20° | B. | 30° | C. | 45° | D. | 60° |
16.在一个不透明的盒子中装有涂颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出一个球是黑球的概率是$\frac{3}{4}$,求m的值.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 3 | 2 |
17.给出四个数0,$\sqrt{5}$,$\frac{2}{7}$,-4,其中是无理数的是( )
| A. | 0 | B. | $\sqrt{5}$ | C. | $\frac{2}{7}$ | D. | -4 |
 如图,已知在平面直角坐标系中,点B在x轴上,半径为3的⊙B与y轴相切,直线l过点A(-2,0),且和⊙B相切,与y轴相交于点C.若点E在直线l上,且以A为圆心,AE为半径的圆与⊙B相切,求点E的坐标.
如图,已知在平面直角坐标系中,点B在x轴上,半径为3的⊙B与y轴相切,直线l过点A(-2,0),且和⊙B相切,与y轴相交于点C.若点E在直线l上,且以A为圆心,AE为半径的圆与⊙B相切,求点E的坐标. 如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE=6.
如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE=6.