题目内容
13.⊙O是等边△ABC的外接圆,⊙O的半径为4,则等边△ABC的边长为( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
分析 连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
解答 解:连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,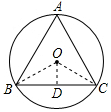
∴∠BOC=$\frac{1}{3}$×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∵⊙O的半径为4,
∴OA=4,
∴BD=OB•cos∠OBD=4×cos30°=2$\sqrt{3}$,
∴BC=4$\sqrt{3}$.
∴等边△ABC的边长为4$\sqrt{3}$,
故选:C.
点评 本题考查的是三角形的外接圆与外心、等边三角形的性质,三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
1. 实数x,y在数轴上的位置如图所示,则( )
实数x,y在数轴上的位置如图所示,则( )
 实数x,y在数轴上的位置如图所示,则( )
实数x,y在数轴上的位置如图所示,则( )| A. | 0<x<y | B. | x<y<0 | C. | x<0<y | D. | y<0<x |
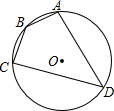 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠D=45°,则劣弧AC的长为π.
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠D=45°,则劣弧AC的长为π. 如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE=6.
如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE=6.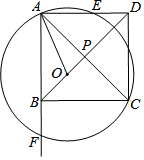 如图,正方形ABCD中,对角线 AC、BD交于点P,O为线段BP上一点(不与B、P重合),以O为圆心OA为半径作⊙O交直线AD、AB于E、F.
如图,正方形ABCD中,对角线 AC、BD交于点P,O为线段BP上一点(不与B、P重合),以O为圆心OA为半径作⊙O交直线AD、AB于E、F.