题目内容
16.无论a取什么实数,点P(a-1,2a-3)都在直线l上.若点Q(m,n)也是直线l上的点,则2m-n+3的值等于( )| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
分析 设直线l的解析式为y=kx+b(k≠0),再分别令a=1,a=2求出P点坐标,进而可得出直线l的解析式,再把点Q(m,n)代入代数式即可得出结论.
解答 解:设直线l的解析式为y=kx+b(k≠0),
∵无论a取什么实数,点P(a-1,2a-3)都在直线l上,
∴当a=1时,P(0,-1),
当a=2时,P(1,1),
∴$\left\{\begin{array}{l}b=-1\\ k+b=1\end{array}\right.$,解得$\left\{\begin{array}{l}b=-1\\ k=2\end{array}\right.$,
∴直线l的解析式为y=2x-1.
∵点Q(m,n)也是直线l上的点,
∴2m-1=n,
∴2m-n+3=2m-(2m-1)+3=4.
故选A.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
6.下列等式正确是( )
| A. | (-2)3=-23 | B. | 23=2×3 | C. | (-2)2=-22 | D. | (-1)2n=-12n |
4.设n为正整数,若64n-7n能被57整除,则82n+1+7n+2能被下列哪个数整除( )
| A. | 55 | B. | 56 | C. | 57 | D. | 58 |
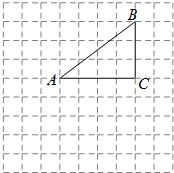 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.