题目内容
18. 如图,AB为⊙O的弦,AB=8,OA=5,OP⊥AB于P,则OP=3.
如图,AB为⊙O的弦,AB=8,OA=5,OP⊥AB于P,则OP=3.
分析 根据垂径定理求出AP=$\frac{1}{2}$AB,根据勾股定理求出OP即可.
解答 解:∵OP⊥AB,OP过O,
∴∠OPA=90°,AP=$\frac{1}{2}$AB,
∵AB=8,
∴AP=4,
由勾股定理得:OP=$\sqrt{A{O}^{2}-A{P}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
故答案为:3.
点评 本题考查了垂径定理和勾股定理的应用,能根据垂径定理求出AP是解此题的关键,垂直于弦的直径平分这条弦.

练习册系列答案
相关题目
9.有一个数值转换器,原理如下:

当输入的x=64时,输出的y等于( )

当输入的x=64时,输出的y等于( )
| A. | 2 | B. | 8 | C. | $2\sqrt{2}$ | D. | $3\sqrt{2}$ |
13.已知:在Rt△ABC中,∠C=90°,sinA=$\frac{3}{4}$,则cosB的值为( )
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
10.已知一次函数y=(m+3)x-2中,y的值随x的增大而增大,则m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m>-3 | D. | m<-3 |
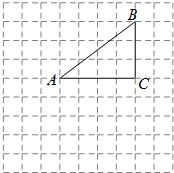 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.