题目内容
13.不等式组$\left\{\begin{array}{l}{\frac{x+1}{3}≤1}\\{1-2x<4}\end{array}\right.$的整数解是-1,0,1,2.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{\frac{x+1}{3}≤1①}\\{1-2x<4②}\end{array}\right.$,
∵解不等式①得:x≤2,
解不等式②得:x>-1.5,
∴不等式组的解集为-1.5<x≤2,
∴不等式组的整数解为:-1,0,1,2,
故答案为:-1,0,1,2.
点评 本题考查了解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
3.某班有50名同学,期末考试优秀的学生人数及科目如表:
这里,一科优秀者包括两、三科优秀者,两科优秀者里也包括三科优秀者,试说明上述统计表的错误.
| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
8.-$\frac{1}{3}$的绝对值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 0 |
2.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
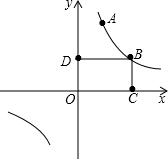 如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.
如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.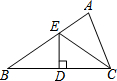 如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )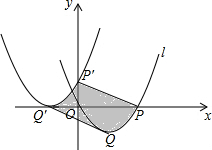 如图,抛物线l:y=2x2-2x,将该抛物线向左并向上平移,使顶点Q的对应点是Q′,抛物线l与x轴的右交点P的对应点是P′,点P′、Q′都在坐标轴上,则在这个平移的过程中,抛物线l上曲线段PQ扫过的面积(即图中阴影部分的面积)为$\frac{3}{4}$.
如图,抛物线l:y=2x2-2x,将该抛物线向左并向上平移,使顶点Q的对应点是Q′,抛物线l与x轴的右交点P的对应点是P′,点P′、Q′都在坐标轴上,则在这个平移的过程中,抛物线l上曲线段PQ扫过的面积(即图中阴影部分的面积)为$\frac{3}{4}$.