题目内容
17．AD是等腰直角三角形ABC一边BC边上的中线（如图），沿AD按（2）所示折叠，设AB与DC相交于点G，试问：△AGC和△BGD的面积有什么关系？为什么？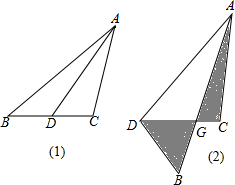
分析 根据等底同高的两三角形面积相等可知：S△ADB=△ADC，然后依据等式的性质即可得出△AGC和△BGD的面积相等．
解答 解：∵AD是△ABC一边BC上的中线，
∴BD=DC．
∴S△ADB=S△ADC．
∴S△ADB-S△ADG=S△ADC-S△ADG．
∴S△AGC=S△BGD．
点评 本题主要考查的是翻折的性质、三角形面积的计算，明确三角形的中线将原三角形分成两个面积相等的三角形是解题的关键．
练习册系列答案
相关题目
如图，△ABC内接于圆O，点A，B，C把圆O的周长三等分．
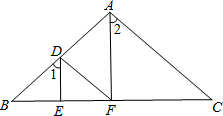如图，已知DE平分∠BDF，AF平分∠BAC，且∠1=∠2，试判断AC与DF的关系，并说明理由．
某Wi-Fi热点的信号覆盖区域是以这个Wi-Fi热点为圆心，r为半径的圆（包括圆的内部），如图为某广场的平面示意图，16个长25m，宽15m的展区排列在面积为9600m2的矩形ABCD区域，展区间纵向横向的每条路宽均相等．