题目内容
6.请先观察下列等式:$\root{3}{2\frac{2}{7}}$=2$\root{3}{\frac{2}{7}}$,$\root{3}{3\frac{3}{26}}$=3$\root{3}{\frac{3}{26}}$,$\root{3}{4\frac{4}{63}}$=4$\root{3}{\frac{4}{63}}$,再写出满足上述各式规律的一般化的公式,并说明.分析 观察等式:左边的被开方数的整数部分和分数部分的分子相同,分母是分子的立方减去1;右边根号外是左边的整数部分,根号内是左边被开方数的分数部分.
解答 解:$\root{3}{(n+1)+\frac{n+1}{(n+1)^{3}-1}}$=(n+1)$\root{3}{\frac{n+1}{(n+1)^{3}-1}}$.
验证:$\root{3}{(n+1)+\frac{n+1}{(n+1)^{3}-1}}$
=$\root{3}{\frac{(n+1)[(n+1)^{3}-1+1]}{(n+1)^{3}-1}}$
=$\root{3}{\frac{(n+1)^{3}(n+1)}{(n+1)^{3}-1}}$
=(n+1)$\root{3}{\frac{n+1}{(n+1)^{3}-1}}$.
点评 此题考查了立方根,等式的规律问题,要分别观察等式的左边和右边.

练习册系列答案
相关题目
16. 为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:
为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:
(1)求出a,b,c的值;
(2)写出这次射击比赛成绩的众数与中位数.
 为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:
为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:| 平均成绩 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | a | 3 | 3 | b | 4 | c | 6 | 1 | 0 |
(2)写出这次射击比赛成绩的众数与中位数.
 如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?
如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?
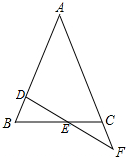 如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗?
如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗? 如图,⊙O直径AB=13cm,C为⊙O上的一点,已知CD⊥AB,垂足为D,并且CD=6cm,AD<DB,求AD的长.
如图,⊙O直径AB=13cm,C为⊙O上的一点,已知CD⊥AB,垂足为D,并且CD=6cm,AD<DB,求AD的长. 如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.
如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.