题目内容
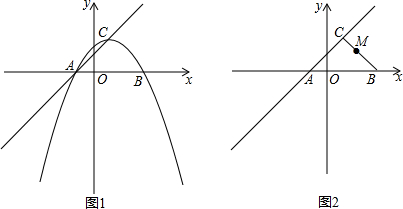
2.已知抛物线y=ax2+bx+c与x轴交于不同的两点A(x1,0)和B(x2,0),与y轴的正半轴交于点C(0,4),如果x1,x2是方程x2-x-6=0的两个根(x1<x2),则△ABC的面积是10.分析 首先解方程求得x1=3,x2=-2,从而得到AB=5,故此三角形的底边长为5,由点C的坐标为(0,4)可知三角形的高为4,然后依据三角形的面积公式计算即可.
解答 解:∵x2-x-6=0,
∴(x-3)(x+2)=0.
∴x1=3,x2=-2.
∴点A的坐标为(-2,0),点B的坐标为(3,0).
∴AB=5.
∵点C的坐标为(0,4),
∴OC=4.
∴△ABC的面积=$\frac{1}{2}AB•OC=\frac{1}{2}×5×4$=10.
故答案为:10.
点评 本题主要考查的是抛物线与x轴的交点,求得点A、B的坐标是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图是成都市某街道的一座人行天桥的示意图,天桥的高是10米,坡面AC的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度,使新坡面DC的倾斜角为30°,若新坡脚前需留3米的人行道,问高原坡脚10米的建筑物EF是否需要拆除?请说明理由.(参考数据:$\sqrt{3}≈1.732$,$\sqrt{2}≈1.414$.)
如图是成都市某街道的一座人行天桥的示意图,天桥的高是10米,坡面AC的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度,使新坡面DC的倾斜角为30°,若新坡脚前需留3米的人行道,问高原坡脚10米的建筑物EF是否需要拆除?请说明理由.(参考数据:$\sqrt{3}≈1.732$,$\sqrt{2}≈1.414$.)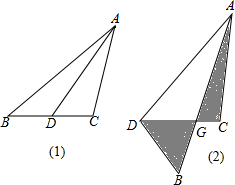
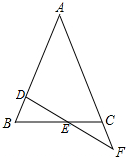 如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗?
如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗?