题目内容
8. 如图,△ABC内接于圆O,点A,B,C把圆O的周长三等分.
如图,△ABC内接于圆O,点A,B,C把圆O的周长三等分.(1)试判断△ABC的形状,并说明理由;
(2)求∠AOB的度数.
分析 (1)利用在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等,可得结论;
(2)由在同圆或等圆中,如果两条弧则圆心角相等,可得∠BOC=∠AOC=∠AOB,∠AOB=360°÷3=120°.
解答 解:(1)△ABC为等边三角形;
∵△ABC内接于圆O,点A,B,C把圆O的周长三等分,
∴$\widehat{AB}=\widehat{AC}=\widehat{BC}$,
∴AB=AC=BC,
∴△ABC为等边三角形;
(2)∵$\widehat{AB}=\widehat{AC}=\widehat{BC}$,
∴∠BOC=∠AOC=∠AOB,
∴∠AOB=360°÷3=120°.
点评 本题主要考查了圆心角,弧,弦的关系,熟练掌握在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等是解答此题的关键.

练习册系列答案
相关题目
18.下列多项式中,在有理数范围内不能用平方差公式分解因式的是( )
| A. | -x2+y2 | B. | 4a2-(a+b)2 | C. | -a2-9b2 | D. | x2y2-1 |
3.关于x的方程5x+m-2=2x的解为正数,则m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | m<2 |
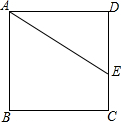 如图,在正方形ABCD中,点E在边DC上,DE=3,EC=2,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为2或8.
如图,在正方形ABCD中,点E在边DC上,DE=3,EC=2,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为2或8. 如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?
如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?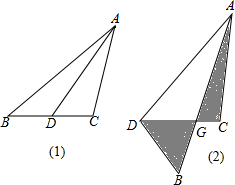
 如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.
如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.