题目内容
9．
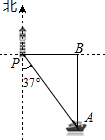如图，一艘海轮位于灯塔P的南偏东37°方向，距离灯塔40 海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的正东方向上的B处．这时，B处与灯塔P的距离BP的长可以表示为（ ）| A． | 40海里 | B． | 40tan37°海里 | C． | 40cos37°海里 | D． | 40sin37°海里 |
分析 根据已知条件得出∠BAP=37°，再根据AP=40海里和正弦定理即可求出BP的长．
解答 解：∵一艘海轮位于灯塔P的南偏东37°方向，
∴∠BAP=37°，
∵AP=40海里，
∴BP=AP•sin37°=40sin37°海里；
故选D．
点评 本题考查解直角三角形，用到的知识点是方位角、直角三角形、锐角三角函数的有关知识，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．
练习册系列答案
相关题目
19．
如图，E是AB上一点，F是DC上一点，G是BC延长线上一点，下列能判断AB∥CD的是（ ）
如图，E是AB上一点，F是DC上一点，G是BC延长线上一点，下列能判断AB∥CD的是（ ）| A． | ∠A+∠B=180° | B． | ∠D=∠DCG | C． | ∠B=∠DCG | D． | ∠B=∠AEF |
17．
如图，点E、F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加一个条件是（ ）
如图，点E、F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加一个条件是（ ）| A． | AD∥BC | B． | DF∥BE | C． | ∠D=∠B | D． | ∠A=∠C |
1．抛物线y=$\frac{1}{2}$x2的图象向左平移2个单位，在向下平移1个单位，得到的函数表达式为（ ）
| A． | y=$\frac{1}{2}$x2+2x+1 | B． | y=$\frac{1}{2}$x2+2x-2 | C． | y=$\frac{1}{2}$x2-2x-1 | D． | y=$\frac{1}{2}$x2-2x+1 |
18．
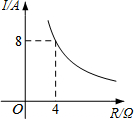已知一块蓄电池的电压为定值，以此蓄电池为电源时，电流I（A）与电阻R（Ω）之间的函数关系如图，则电流I关于电阻R的函数解析式为（ ）
已知一块蓄电池的电压为定值，以此蓄电池为电源时，电流I（A）与电阻R（Ω）之间的函数关系如图，则电流I关于电阻R的函数解析式为（ ）| A． | $I=\frac{4}{R}$ | B． | $I=\frac{8}{R}$ | C． | $I=\frac{32}{R}$ | D． | $I=-\frac{32}{R}$ |
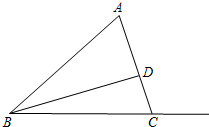已知：△ABC中，AB=13，AC=9，BC=4$\sqrt{10}$，BD⊥AC于D．