题目内容
20.若等腰三角形的两条边长分别为1和2,则这个等腰三角形的周长是5.分析 题目给出等腰三角形有两条边长为1和2,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:当腰为2时,周长=2+2+1=5;
当腰长为1时,1+1=2不能组成三角形.
故答案为:5.
点评 本题考查的是等腰三角形的性质和三角形的三边关系,已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.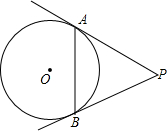 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )| A. | 60° | B. | 120° | C. | 30°或120° | D. | 60°或120° |
8.下列关于x的方程中,一定是一元二次方程的为( )
| A. | 2x+3=0 | B. | x2-2=(x+3)2 | C. | ${x^2}=\frac{1}{x}$ | D. | x2-1=0 |
15. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )| A. | ∠A=∠D | B. | ∠B=∠E | C. | AC=DC | D. | AB=DE |
9.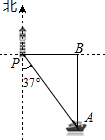 如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
 如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )| A. | 40海里 | B. | 40tan37°海里 | C. | 40cos37°海里 | D. | 40sin37°海里 |
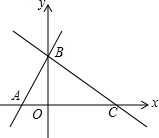 如图,一次函数y=(m-1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4.
如图,一次函数y=(m-1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4. 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.