题目内容
1．抛物线y=$\frac{1}{2}$x2的图象向左平移2个单位，在向下平移1个单位，得到的函数表达式为（ ）| A． | y=$\frac{1}{2}$x2+2x+1 | B． | y=$\frac{1}{2}$x2+2x-2 | C． | y=$\frac{1}{2}$x2-2x-1 | D． | y=$\frac{1}{2}$x2-2x+1 |
分析 根据“上加下减，左加右减”的原则进行解答即可．
解答 解：根据“上加下减，左加右减”的原则可知，
二次函数y=$\frac{1}{2}$x2的图象向左平移2个单位，再向下平移1个单位得到的图象表达式为
y=$\frac{1}{2}$（x+2）2-1，
即y=$\frac{1}{2}$x2+2x+1．
故选A．
点评 本题考查的是二次函数的图象与几何变换，熟知“上加下减，左加右减”的原则是解答此题的关键．
练习册系列答案
相关题目
11．
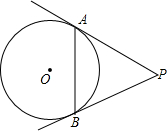如图，PA、PB是圆O的切线，切点分别是A、B，如果∠P=60°，那么弦AB所对的圆周角等于（ ）
如图，PA、PB是圆O的切线，切点分别是A、B，如果∠P=60°，那么弦AB所对的圆周角等于（ ）| A． | 60° | B． | 120° | C． | 30°或120° | D． | 60°或120° |
9．
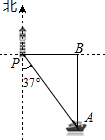如图，一艘海轮位于灯塔P的南偏东37°方向，距离灯塔40 海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的正东方向上的B处．这时，B处与灯塔P的距离BP的长可以表示为（ ）
如图，一艘海轮位于灯塔P的南偏东37°方向，距离灯塔40 海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的正东方向上的B处．这时，B处与灯塔P的距离BP的长可以表示为（ ）| A． | 40海里 | B． | 40tan37°海里 | C． | 40cos37°海里 | D． | 40sin37°海里 |
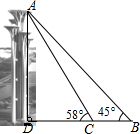奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成．在综合实践活动课中，某小组的同学决定利用测角仪测量这五座塔中最高塔的高度（测角仪高度忽略不计）．他们的操作方法如下：如图，他们先在B处测得最高塔塔顶A的仰角为45°，然后向最高塔的塔基直行90米到达C处，再次测得最高塔塔顶A的仰角为58°．请帮助他们计算出最高塔的高度AD约为多少米．（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）
在平面直角坐标系xOy中，抛物线y=x2+bx+c经过点A（-1，t），B（3，t），与y轴交于点C（0，-1）．一次函数y=x+n的图象经过抛物线的顶点D．