题目内容
19.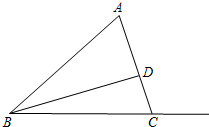 已知:△ABC中,AB=13,AC=9,BC=4$\sqrt{10}$,BD⊥AC于D.
已知:△ABC中,AB=13,AC=9,BC=4$\sqrt{10}$,BD⊥AC于D.(1)求线段BD的长;
(2)点P为射线BC上一动点,若△BDP为等腰三角形,求BP的长.
分析 (1)设AD=x,则CD=9-x,由勾股定理得出方程${13^2}-{x^2}={({4\sqrt{10}})^2}-{({9-x})^2}$,解方程求出AD,再由勾股定理求出BD即可;
(2)分三种情况讨论:①若BD=BP,则BP=12;
②若DP=DB,过点D作DE⊥BC于点E,由三角形的面积求出DE,由勾股定理求出BE,即可得出BP的长;
③若PD=PB,则∠1=∠2,求出∠3=∠4,得出PD=PC,因此BP=PC,即可得出结果.
解答 解:(1)设AD=x,则CD=9-x,∵BD⊥AC,∴∠ADB=∠BDC=90°,
由勾股定理得:AB2-AD2=BD2=BC2-CD2,
∴${13^2}-{x^2}={({4\sqrt{10}})^2}-{({9-x})^2}$,
解得:x=5,
∴BD=$\sqrt{A{B^2}-A{D^2}}$=12;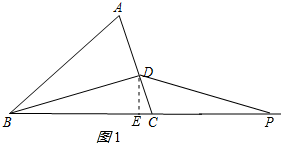
(2)∵△BDP为等腰三角形,
∴分三种情况:
①若BD=BP,则BP=12,
②若DP=DB,
过点D作DE⊥BC于点E,如图1所示:
∵${S_{△BDC}}=\frac{1}{2}BD•CD=\frac{1}{2}BC•DE$
∴$DE=\frac{BD•CD}{BC}=\frac{12×4}{{4\sqrt{10}}}=\frac{6}{5}\sqrt{10}$,
∴$BE=\sqrt{B{D^2}-D{E^2}}=\frac{18}{5}\sqrt{10}$,
∵BD=DP且DE⊥BC,
∴BP=2BE=$\frac{36}{5}$$\sqrt{10}$,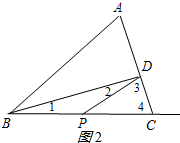
③若PD=PB,如图2所示:
∵PD=BP,
∴∠1=∠2,
∵∠BDC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
∴∠3=∠4
∴PD=PC,
∴BP=PC,
∴BP=$\frac{1}{2}$BC=$2\sqrt{10}$,
综上所述:当△BDP为等腰三角形时,BP=12或$\frac{36}{5}$$\sqrt{10}$或$2\sqrt{10}$.
点评 本题考查了勾股定理、等腰三角形的判定与性质;熟练掌握等腰三角形的性质,运用勾股定理得出方程和进行计算是解决问题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案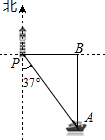 如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )| A. | 40海里 | B. | 40tan37°海里 | C. | 40cos37°海里 | D. | 40sin37°海里 |

| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
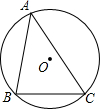 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )| A. | 发生变化,随A位置决定 | B. | 不变,等于2 | ||
| C. | 有最大值为2$\sqrt{3}$ | D. | 有最小值为1 |
 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D. 如图是正方体的一种展开图,其每个面上都标有数字,那么在原正方体中,与数字“2”相对的面上的数字是( )
如图是正方体的一种展开图,其每个面上都标有数字,那么在原正方体中,与数字“2”相对的面上的数字是( )