题目内容
11.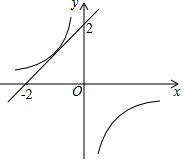 在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )| A. | m>2 | B. | -2<m<2 | C. | m<-2 | D. | m>2或m<-2 |
分析 根据反比例函数的对称性即可得知:直线y=x-2与反比例函数y=-$\frac{k}{x}$的图象有唯一公共点,结合函数图象即可得出当直线y=x+m在直线y=x+2的上方或直线y=x+m在直线y=x-2的下方时,直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,由此即可得出m的取值范围.
解答 解:根据反比例函数的对称性可知:直线y=x-2与反比例函数y=-$\frac{k}{x}$的图象有唯一公共点,
∴当直线y=x+m在直线y=x+2的上方或直线y=x+m在直线y=x-2的下方时,直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,
∴m>2或m<-2.
故选D.
点评 本题考查了反比例函数与一次函数的交点问题,根据反比例函数的对称性找出直线y=x-2与反比例函数y=-$\frac{k}{x}$的图象有唯一公共点是解题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1.如果P点的坐标为(a,b),它关于y轴的对称点为P1,P1关于x轴的对称点为P2,已知P2的坐标为(-2,3),则点P的坐标为( )
| A. | (2,-3) | B. | (-2,-3) | C. | (-2,3) | D. | (2,3) |
6.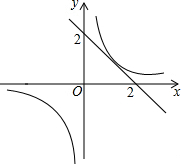 如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )
如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )
 如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )
如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )| A. | b>2 | B. | -2<b<2 | C. | b>2或b<-2 | D. | b<-2 |
3.抛物线y=-(a-8)2+2的顶点坐标是( )
| A. | ( 2,8 ) | B. | ( 8,2 ) | C. | (-8,2 ) | D. | (-8,-2) |
20.已知一次函数y1=kx+b(k<0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2,实数x的取值范围是( )
| A. | x<-1或0<x<3 | B. | -1<x<0或0<x<3 | C. | -1<x<0或x>3 | D. | 0<x<3 |
5.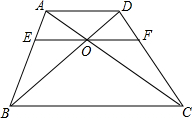 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )| A. | $\frac{m+n}{mn}$ | B. | $\frac{2mn}{m+n}$ | C. | $\frac{mn}{m+n}$ | D. | $\frac{m+n}{2mn}$ |
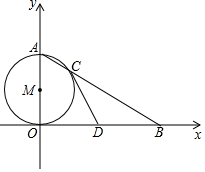 如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.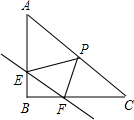 如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=$\frac{6}{5}$,BC=$\frac{8}{5}$.
如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=$\frac{6}{5}$,BC=$\frac{8}{5}$.