题目内容
5.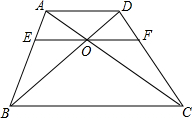 如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )
如图,四边形ABCD,AD∥BC,AD=m,BC=n,EF∥AD,经过点O,求EF的长为( )| A. | $\frac{m+n}{mn}$ | B. | $\frac{2mn}{m+n}$ | C. | $\frac{mn}{m+n}$ | D. | $\frac{m+n}{2mn}$ |
分析 根据已知条件和平行线分线段成比例定理分别表示出OE和OF的长,从而得出答案.
解答 解:∵AD∥BC,AD=m,BC=n,
∴$\frac{AD}{BC}$=$\frac{AO}{OC}$=$\frac{m}{n}$,
∴$\frac{OC}{AC}$=$\frac{n}{m+n}$,$\frac{OA}{AC}$=$\frac{m}{m+n}$,
∵EF∥AD,
∴$\frac{OF}{AD}$=$\frac{OC}{AC}$,EF∥BC,
∴$\frac{OF}{m}$=$\frac{n}{m+n}$,$\frac{OE}{BC}$=$\frac{OA}{AC}$,
∴OF=$\frac{mn}{m+n}$,$\frac{OE}{n}$=$\frac{m}{m+n}$,
∴OE=$\frac{mn}{m+n}$,
∴EF=OE+OF=$\frac{mn}{m+n}$+$\frac{mn}{m+n}$=$\frac{2mn}{m+n}$;
故选B.
点评 此题考查了平行线分线段成比例定理,找准对应关系,列出相应的比例式是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
11.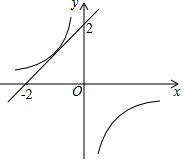 在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
 在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )| A. | m>2 | B. | -2<m<2 | C. | m<-2 | D. | m>2或m<-2 |
9.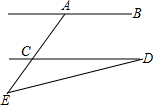 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )| A. | 24° | B. | 26° | C. | 34° | D. | 22° |
16. 在平面直角坐标系内,作出下列函数的图象.
在平面直角坐标系内,作出下列函数的图象.
(1)如图,y=-x+2.5,填写表,并在图中的坐标系上描点、连线并回答问题.
①当x=3时,y=-0.5;当y=0时,x=2.5.
②图象与x轴的交点坐标是(2.5,0),与y轴的交点坐标是(0,2.5).
③点A(-3,1.5),B(0.5,2)是否在函数图象上?
 在平面直角坐标系内,作出下列函数的图象.
在平面直角坐标系内,作出下列函数的图象.(1)如图,y=-x+2.5,填写表,并在图中的坐标系上描点、连线并回答问题.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4.5 | 3.5 | 2.5 | 1.5 | 0.5 | … |
②图象与x轴的交点坐标是(2.5,0),与y轴的交点坐标是(0,2.5).
③点A(-3,1.5),B(0.5,2)是否在函数图象上?