题目内容
20.已知一次函数y1=kx+b(k<0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2,实数x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或0<x<3 | C. | -1<x<0或x>3 | D. | 0<x<3 |
分析 根据题意画出函数图象,根据两函数图象的上下位置关系即可得出不等式的解集.
解答 解:依照题意画出函数图象,如图所示.
观察函数图象,可知:当x<-1或0<x<3时,一次函数图象在反比例函数图象上方,
∴当y1>y2,实数x的取值范围为x<-1或0<x<3.
故选A.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象以及反比例函数图象,根据题意画出函数图象,利用数形结合解不等式是解题的关键.

练习册系列答案
相关题目
11.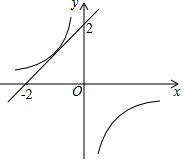 在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
 在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )
在平面直角坐标系中直线y=x+2与反比例函数 y=-$\frac{k}{x}$的图象有唯一公共点,若直线y=x+m与反比例函数y=-$\frac{k}{x}$的图象有2个公共点,则m的取值范围是( )| A. | m>2 | B. | -2<m<2 | C. | m<-2 | D. | m>2或m<-2 |
8.已知x2-2x-3=0,则2x2-4x的值为( )
| A. | 6 | B. | -6 | C. | -2或6 | D. | -2或30 |
9.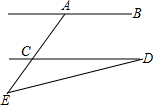 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )| A. | 24° | B. | 26° | C. | 34° | D. | 22° |
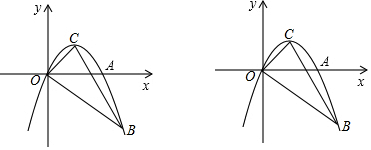
 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )


