题目内容
5.某租赁公司拥有20辆小型汽车,公司平均每日的各项支出共6250元,当每辆车的日租金为500元时,可全部租出:当每辆车的日租金每增加50元,未租出的车将增加1辆.根据以上材料解答下列问题:设公司每日租出x辆车时,日收益为y元(日收益=日租金收入-平均每日各项支出).(1)公司每日租出x辆车时,每辆车的日租金收入为1500-50x元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益才能盈利?
分析 (1)由题意可得,每辆车的日租金收入为:500+(20-x)×50,从而可以解答本题;
(2)根据日收益=日租金收入-平均每日各项支出,可以得出租赁公司日收益,从而可以解答本题;
(3)令第(2)问中的收益的式子大于0,即可求问题的答案.
解答 解:(1)由题意可得,
每辆车的日租金收入为:500+(20-x)×50=500+1000-50x=1500-50x.
故答案为:1500-50x;
(2)由题意可得,
租金公司的日收益为:x(1500-50x)-6250=-50(x-15)2+5000,
∵-50<0,
∴-50(x-15)2+5000有最大值,此时,x=15,最大值为:5000,
即每日租出15辆时,租赁公司日收益最大,最大是5000元;
(3)-50(x-15)2+5000>0,
解得5<x<25,
∵x≤20,
∴5<x≤20,
即当每日租出至少6辆时,租赁公司的日收益才能盈利.
点评 本题考查二次函数的应用,解题的关键是明确题意可以列出相应的函数关系式,会求函数的最值,解不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.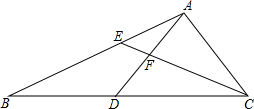 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
17.已知a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$+$\frac{1}{b-c}$.则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |

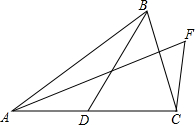 如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.
如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.