题目内容
17.已知a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$+$\frac{1}{b-c}$.则M与N的大小关系为( )| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
分析 求M与N的大小,只要把M与N作差即可,看最终的结果即可解答本题.
解答 解:∵a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$+$\frac{1}{b-c}$,
∴M-N
=$\frac{2}{a-c}-(\frac{1}{a-b}+\frac{1}{b-c})$
=$\frac{2}{a-c}-\frac{1}{a-b}-\frac{1}{b-c}$
=$\frac{2(a-b)(b-c)-(a-c)(b-c)-(a-c)(a-b)}{(a-c)(a-b)(b-c)}$
=$\frac{(b-c)[(a-b)-(a-c)]+(a-b)[(b-c)-(a-c)]}{(a-c)(a-b)(b-c)}$
=$\frac{-(b-c)^{2}-(a-b)^{2}}{(a-c)(a-b)(b-c)}$
∵a>b>c,
∴a-c>0,a-b>0,b-c>0,-(b-c)2<0,-(a-b)2<0,
∴$\frac{-(b-c)^{2}-(a-b)^{2}}{(a-c)(a-b)(b-c)}$<0,
∴M-N<0,
即M<N.
故选C.
点评 本题考查分式的加减法,解题的关键是M与N作差之后,由a>b>c,可以判断M与N的大小.

练习册系列答案
相关题目
8.如果点A(2,m)在抛物线y=x2上,将抛物线向右平移3个单位后,点A同时平移到点A′,那么A′坐标为( )
| A. | (2,1) | B. | (2,7) | C. | (5,4) | D. | (-1,4) |
12.在同一平面直角坐标系内,将函数y=x-3的图象向右平移2个单位,再向下平移1个单位得到的图象与x轴的交点坐标是( )
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
12.沿海产业基地明湖广场占地面积约为14500m2,用科学记数法表示为( )
| A. | 1.45×106m2 | B. | 145×103m2 | C. | 1.45×104m2 | D. | 14.5×104m2 |
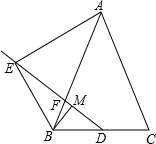 如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.
如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.