题目内容
20.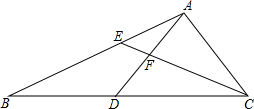 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
分析 (1)根据等腰三角形的性质得到∠B=∠BAD,∠ADC=∠ACD,推出△EAF∽△ECA,根据相似三角形的性质得到∠EAF=∠ECA,于是得到∠ADC=∠ACD=∠ACE+∠ECB=∠DCE+∠EAF;
(2)根据相似三角形的性质得到$\frac{AE}{EF}=\frac{AC}{AF}$,即$\frac{AF}{EF}=\frac{AC}{AE}$,推出△FAE∽△ABC,根据相似三角形的性质得到$\frac{FA}{AB}=\frac{EF}{AC}$,于是得到FA•AC=EF•AB,等量代换即可得到结论.
解答 证明:(1)∵BD=AD=AC,
∴∠B=∠BAD,∠ADC=∠ACD,
∵AE2=EF•EC,
∴$\frac{AE}{CE}=\frac{EF}{AE}$,
∵∠E=∠E,
∴△EAF∽△ECA,
∴∠EAF=∠ECA,
∴∠ADC=∠ACD=∠ACE+∠ECB=∠DCE+∠EAF;
(2)∵△EAF∽△ECA,
∴$\frac{AE}{EF}=\frac{AC}{AF}$,即$\frac{AF}{EF}=\frac{AC}{AE}$,
∵∠EFA=∠BAC,∠EAF=∠B,
∴△FAE∽△ABC,
∴$\frac{FA}{AB}=\frac{EF}{AC}$,
∴FA•AC=EF•AB,
∵AC=AD,
∴AF•AD=AB•EF.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,三角形的外角的性质,证得△EAF∽△ECA是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
8.如果点A(2,m)在抛物线y=x2上,将抛物线向右平移3个单位后,点A同时平移到点A′,那么A′坐标为( )
| A. | (2,1) | B. | (2,7) | C. | (5,4) | D. | (-1,4) |
12.在同一平面直角坐标系内,将函数y=x-3的图象向右平移2个单位,再向下平移1个单位得到的图象与x轴的交点坐标是( )
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
15. 如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
 如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )
如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值范围是( )| A. | -2<b<0 | B. | -1<b<0 | C. | -$\frac{1}{2}$<b<0 | D. | 0<b<0 |
 如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.
如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.