题目内容
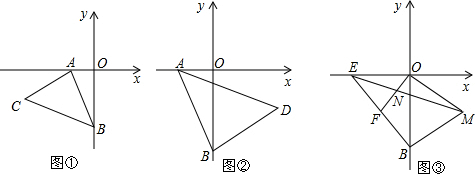
14.如图1,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P,Q两点),设∠AOB=α.(1)当α=60°时,判断线段AB所在的直线与圆O的位置关系,并说明理由;
(2)当线段AB与圆O只有一个公共点(即A点)时,求α的范围(直接写出答案);
(3)当线段AB与圆O有两个公共点A,M时(如图2),若AM=1,求阴影部分的面积.

分析 (1)连结AQ,证明△OAQ是等边三角形,得出∠OAQ=∠AQO=60°,AQ=OQ,证出AQ=QB,由三角形的外角性质和等腰三角形的性质得出∠B=∠BAQ=$\frac{1}{2}$∠AQO=30°,求出∠OAQ=90°,即可得出结论;
(2)当点A在Q点时,易得α=0°,当点A为切点,由(1)得α=60°,于是可判断线段AB与圆O只有一个公共点(即A点)时,0≤α≤60°.
(3)连接OM,证明△AOM是等边三角形,得出∠AOM=60°,作ON⊥AB于N,则AN=$\frac{1}{2}$AM=$\frac{1}{2}$,求出ON=$\sqrt{3}$AN=$\frac{\sqrt{3}}{2}$,阴影部分的面积=扇形AOM的面积-△AOM的面积,即可得出结果.
解答 解: (1)线段AB所在的直线与圆O相切;理由如下:
(1)线段AB所在的直线与圆O相切;理由如下:
连结AQ,如图1所示:
∵∠AOB=α=60°,OA=OQ,
∴△OAQ是等边三角形,
∴∠OAQ=∠AQO=60°,AQ=OQ,
∵OQ=QB,
∴AQ=QB,
∴∠B=∠BAQ=$\frac{1}{2}$∠AQO=30°,
∴∠OAQ=60°+30°=90°,
∴线段AB所在的直线与圆O相切;
(2)当点A在Q点时,α=0°,
当点A为线段AB的所在的直线与⊙O相切时切点,
由(1)得α=60°,
所以当线段AB与圆O只有一个公共点(即A点)时,0≤α≤60°.
(3)连接OM,如图2所示:
∵AM=1,OQ=OA=1,
∴△AOM是等边三角形,
∴∠AOM=60°,
作ON⊥AB于N,
则AN=$\frac{1}{2}$AM=$\frac{1}{2}$,
∴ON=$\sqrt{3}$AN=$\frac{\sqrt{3}}{2}$,
∴阴影部分的面积=扇形AOM的面积-△AOM的面积=$\frac{60•π×{1}^{2}}{360}$-$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$.
点评 本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了扇形的面积公式.

 名校课堂系列答案
名校课堂系列答案| A. | 1,5 | B. | 1,-6 | C. | 5,-6 | D. | 5,6 |
| A. | 平行四边形 | B. | 三角形 | C. | 圆 | D. | 梯形 |