题目内容
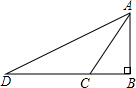
13．△ABC中，AB=20，AC=13，BC上的高为12，求BC的长．分析 根据题意正确画出图形进而结合当D在线段BC上时以及当D在线段BC的延长线上时，分别得出答案．
解答 解：如图1所示：
在Rt△ABD中，AB=20，AD=12，
根据勾股定理：BD=$\sqrt{2{0}^{2}-1{2}^{2}}$=16；
在Rt△ACD中，AC=13，AD=12，
根据勾股定理：CD=$\sqrt{1{3}^{2}-1{2}^{2}}$=5；
当D在线段BC上时，BC=16+5=21；
如图2所示：
当D在线段BC的延长线上时，BC=16-5=11，
综上所述：BC=21或11．
点评 此题主要考查了勾股定理，根据题意正确画出图形利用分类讨论得出是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
在图的方格纸中画出△ABC关于y轴对称的图形．
8．下列计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ | C． | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | D． | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
如图，某人要测一建筑物AB的高度，他在地面D处测得建筑物顶端A的仰角为30°，沿AE方向前进100米到达点C处，测得建筑物的顶端A的仰角为45°，求建筑物的高．
如图，皋兰山某处有一座信号塔AB，山坡BC的坡度为1：$\sqrt{3}$，现为了测量塔高AB，测量人员选择山坡C处为一测量点，测得∠DCA=45°，然后他顺山坡向上行走100米到达E处，再测得∠FEA=60°．