题目内容
8.下列计算正确的是( )| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ | C. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
分析 根据二次根式的加减法则对各选项进行逐一分析即可.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不是同类项,不能合并,故本选项错误;
B、5$\sqrt{5}$与2$\sqrt{2}$不是同类项,不能合并,故本选项错误;
C、2$\sqrt{3}$×3$\sqrt{3}$=18≠6$\sqrt{3}$,故本选项错误;
D、$\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,故本选项正确.
故选D.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
20.一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了1000次,其中有200次摸到白球,因此小亮估计口袋中的红球大约为( )
| A. | 60个 | B. | 50个 | C. | 40个 | D. | 30个 |
18.在下列图象中,能作为一次函数y=-x+1的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
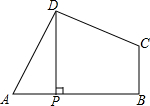 如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.
如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长. 如图,用式子表示圆环的面积.当R=10cm,r=8cm时,求圆环的面积(π取3.14,结果精确到个位).
如图,用式子表示圆环的面积.当R=10cm,r=8cm时,求圆环的面积(π取3.14,结果精确到个位).