Question

5．如图，皋兰山某处有一座信号塔AB，山坡BC的坡度为1：$\sqrt{3}$，现为了测量塔高AB，测量人员选择山坡C处为一测量点，测得∠DCA=45°，然后他顺山坡向上行走100米到达E处，再测得∠FEA=60°．
（1）求出山坡BC的坡角∠BCD的大小；
（2）求塔顶A到CD的铅直高度AD．（结果保留整数：$\sqrt{3}≈1.73，\sqrt{2}≈1.41$）

Answer 1

分析 （1）根据tan∠BCD=$\frac{1}{\sqrt{3}}$，进而得出答案；
（2）设AD=x，则CD=AD=x，可得AF=x-50，EF=x-50$\sqrt{3}$，进而利用在Rt△AEF中，$\frac{AF}{EF}$=tan60°，求出答案．

解答 解：（1）依题意得：tan∠BCD=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
∴∠BCD=30°；

（2）方法1：
作EG⊥CD，垂足为G．
在Rt△CEG中，CE=100，∠ECG=30°，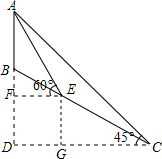
∴EG=CE•sin30°=50，
CG=CE•cos30°=50$\sqrt{3}$，
设AD=x，则CD=AD=x．
∴AF=x-50，EF=x-50$\sqrt{3}$，
在Rt△AEF中，$\frac{AF}{EF}$=tan60°，
∴$\frac{x-50}{x-50\sqrt{3}}$=$\sqrt{3}$．
解得：x=50$\sqrt{3}$+50≈136.5（米）．
答：塔顶A到CD的铅直高度AD约为137米．
方法2：
∵∠ACD=45°，
∴∠ACE=15°．
∵∠AEF=60°，
∴∠EAF=30°．
∵∠DAC=45°，
∴∠EAC=∠DAC-∠EAF=15°，
∴∠ACE=∠EAC．
∴AE=CE=100．
在Rt△AEF中，∠AEF=60°，
∴AF=AE•sin60°=50$\sqrt{3}$（m），
在Rt△CEG中，CE=100m，∠ECG=30°，
∴EG=CE•sin30°=50m．
∴AD=AF+FD=AF+EG=50$\sqrt{3}$+50≈136.5（米）．
答：塔顶A到CD的铅直高度AD约为137米．

点评 此题主要考查了解直角三角形的应用以及坡角的定义，正确构造直角三角形是解题关键．