题目内容
1.线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,还接AE,BD,分别交CD,CA于Q,P.(1)找出图中的几组全等三角形,又有哪几种相等的线段?
(2)取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状.
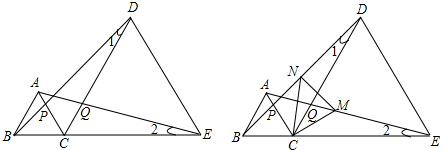
分析 (1)利用等边三角形的性质以及全等三角形的判定得出即可;
(2)利用全等三角形的判定与性质得出△DCN≌△ECM,进而得出∠NCM=60°,利用等边三角形的判定得出即可.
解答 解:∵等边三角形ABC、DCE,
∵∠ACB=∠ACD=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中
$\left\{\begin{array}{l}{BC=CA}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$
∴△BCD≌△ACE(SAS)
∴BD=AE,∠1=∠2,
∵∠ACB=∠DCE=60°,
∴∠PCQ=60°,
在△PCD和△QCE中,
$\left\{\begin{array}{l}{∠1=∠2}\\{CD=CE}\\{∠PCD=∠QCE}\end{array}\right.$
∴△PCD≌△QCE,
∴PC=QC,PD=QE.
∴图中全等的三角形有:△PCD≌△QCE,△BCD≌△ACE;
相等的线段有:AB=AC=BC,DC=CE=DE,BD=AE,PC=QC,PD=QE.
(2)等边三角形.
理由:由△BCD≌△ACE,可得∠1=∠2,BD=AE,M是AE的中点、N是BD的中点,
∴DN=EM,又DC=CE,
在△DCN和△ECM中,
$\left\{\begin{array}{l}{DN=EM}\\{∠1=∠2}\\{DC=EC}\end{array}\right.$,
∴△DCN≌△ECM(SAS),
∴CN=CM,∠NCD=∠MCE,∠MCE+∠DCM=60°,
所以∠NCD+∠DCM=60°,
即∠NCM=60°,
∴△CMN为等边三角形.
点评 此题主要考查了全等三角形的判定与性质和等边三角形的判定与性质,根据已知熟练利用等边三角形的性质得出对应边对应角相等是解题关键.

| A. | 0既不是正数,也不是负数 | B. | 0是绝对值最小的有理数 | ||
| C. | 0℃表示没有温度 | D. | 0是整数,也是有理数,但不是分数 |

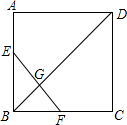 如图,点E、F分别在正方形ABCD的边AB、BC上,EF与对角线BD交于点G,如果BE=5,BF=3,那么FG:EF的比值是$\frac{3}{8}$.
如图,点E、F分别在正方形ABCD的边AB、BC上,EF与对角线BD交于点G,如果BE=5,BF=3,那么FG:EF的比值是$\frac{3}{8}$.