题目内容
2.已知线段AB上有两点C、D,使得AC:CD:DB=1:2:3,M是AC的中点,DN=$\frac{1}{4}$DB,AB=24,求MN的长.分析 先作出图形,根据线段之间的关系求出MC=2,DN=3,然后求出MN的长度即可.
解答 解:如图: ∵线段AB=24,AC:CD:DB=1:2:3,
∵线段AB=24,AC:CD:DB=1:2:3,
∴AC=4,CD=8,DB=12,
∵点M是AC的中点,DN=$\frac{1}{4}$DB,
∴MC=2,DN=3,
∴MN=MC+CD+DN=2+8+3=13.
点评 本题考查了两点间的距离,解答本题的关键是根据题意求出AC、CD、DB的长度.

练习册系列答案
相关题目
13.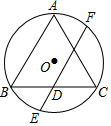 如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )
如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )
 如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )
如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )| A. | 2 | B. | 1.5 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
7.甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况制成如下统计表,依据相关信息,解答下列问题:
(1)在统计表中,工人甲7天出现次品数的众数为2,其极差是4,工人乙7天出现次品数的中位数为1;
(2)根据题目所给数据,通过计算判断甲、乙两名工人谁出现次品的波动要小些;
(3)请估计甲、乙加工该种零件30天共出现次品多少件?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 甲(件) | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙(件) | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
(2)根据题目所给数据,通过计算判断甲、乙两名工人谁出现次品的波动要小些;
(3)请估计甲、乙加工该种零件30天共出现次品多少件?
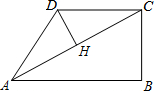 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )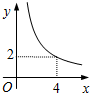
 将长方形ABCD沿EF折叠,得到如图所示的图形,已知∠BEF=50°,则∠AEB′的大小是80度.
将长方形ABCD沿EF折叠,得到如图所示的图形,已知∠BEF=50°,则∠AEB′的大小是80度.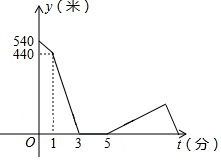 “欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.
“欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.