题目内容
抛物线顶点坐标为(2,6),且经过点(4,2),P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N,设点P横坐标为m,若PN与这条抛物线的另一个交点为点Q,求
≤QN≤1时m的取值范围.
| 1 |
| 3 |
考点:二次函数的性质
专题:计算题
分析:首先求出抛物线解析式,进而表示出P点,Q点横坐标,即可得出QN的长,进而解不等式求出即可.
解答: 解:设抛物线解析式为y=a(x-2)2+6,
解:设抛物线解析式为y=a(x-2)2+6,
∵抛物线经过点(4,2),
∴2=a(4-2)2+6,
解得:a=-1,
∴抛物线为y=-x2+4x+2,
当x=0时,y=2,
∴抛物线与y轴交点为(0,2),
∵P是抛物线上x轴上方一点,且在对称轴右侧,横坐标为m,抛物线对称轴为x=2,
∴Q的横坐标为:m-2(m-2)=4-m,
∴QN=4-m,当
≤QN≤1时,
则
≤4-m≤1,
解得:3≤m≤
.
 解:设抛物线解析式为y=a(x-2)2+6,
解:设抛物线解析式为y=a(x-2)2+6,∵抛物线经过点(4,2),
∴2=a(4-2)2+6,
解得:a=-1,
∴抛物线为y=-x2+4x+2,
当x=0时,y=2,
∴抛物线与y轴交点为(0,2),
∵P是抛物线上x轴上方一点,且在对称轴右侧,横坐标为m,抛物线对称轴为x=2,
∴Q的横坐标为:m-2(m-2)=4-m,
∴QN=4-m,当
| 1 |
| 3 |
则
| 1 |
| 3 |
解得:3≤m≤
| 11 |
| 3 |
点评:本题考查了二次函数的性质以及待定系数法求二次函数解析式和不等式组解法等知识,表示出QN的长是解题关键.

练习册系列答案
相关题目
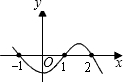 已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )
已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )| A、x<0 |
| B、-1<x<1或x>2 |
| C、x>-1 |
| D、x<-1或1<x<2 |
中国电信公司最近推出的无线市话小灵通的通话收费标准为:前3分钟(不足3分钟按3分钟)为0.2元;3分钟后每分钟收0.1元,则一次通话实际那为x分钟(x>3)与这次通话的费用y(元)之间的函数关系是( )
| A、y=0.2+0.1x |
| B、y=0.1x |
| C、y=-0.1+0.1x |
| D、y=0.5+0.1x |
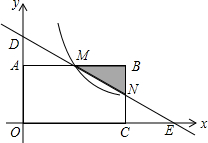 如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
 如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.
如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.