题目内容
当直角三角形的直角顶点P在正方形ABCD对角线AC上运动(P与A、C不重合)且一直角边始终过点D,另一直角边与射线BC交于点E
(1)如图1,当点E与BC边相交时,
①证明:△PBE为等腰三角形;
②写出线段AP、PC与EC之间的等量关系 (并给出证明过程)
(2)当点E在BC的延长线上时,请完成图2,并判断(1)中的①、②结论是否分别成立?若不成立,写出相应的结论(不必证明)

(1)如图1,当点E与BC边相交时,
①证明:△PBE为等腰三角形;
②写出线段AP、PC与EC之间的等量关系
(2)当点E在BC的延长线上时,请完成图2,并判断(1)中的①、②结论是否分别成立?若不成立,写出相应的结论(不必证明)

考点:正方形的性质,全等三角形的判定与性质,等腰三角形的判定与性质
专题:探究型
分析:(1)①先求证△PBC≌△PDC得∠PBC=∠PDC,由∠BCD=∠DPE=90°,∠PEB=∠PDC,∠PEB=∠PBC即可证明PB=PE,即△PBE为等腰三角形;
②过E作EA′垂直于BC,交AC于A',由平行线等分线段定理得PA=PA′,进一步利用等腰直角三角形的性质求得结论;
(2)类比于(1)的结论得出即可.
②过E作EA′垂直于BC,交AC于A',由平行线等分线段定理得PA=PA′,进一步利用等腰直角三角形的性质求得结论;
(2)类比于(1)的结论得出即可.
解答: 解:(1)①∵四边形ABCD是正方形,
解:(1)①∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°,∠BCD=90°,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS).
∴∠PBC=∠PDC.
∵∠BCD=∠DPE=90°
∴∠PDC+∠PEC=180°,又∠PEB+∠PEC=180°
∴∠PEB=∠PDC,
∴∠PEB=∠PBC
∴PB=PE
∴△PBE为等腰三角形.
②EC=
证明:如图1,
过P作PF垂直于BC,过E作EA′∥PF交AC于A',
∵BF=EF,EA′∥PF∥AB,
∴PA=PA′,
在△A′EC中∠A′EC=90°,∠A′CE=45°,
∴△A′EC为等腰直角三角形,
∴A′C=
CE,
∴EC=
=
.
(2)结论①仍成立;
结论②不成立,此时②中三条线段的数量关系是EC=
.
 解:(1)①∵四边形ABCD是正方形,
解:(1)①∵四边形ABCD是正方形,∴BC=DC,∠BCP=∠DCP=45°,∠BCD=90°,
在△PBC和△PDC中,
|
∴△PBC≌△PDC(SAS).
∴∠PBC=∠PDC.
∵∠BCD=∠DPE=90°
∴∠PDC+∠PEC=180°,又∠PEB+∠PEC=180°
∴∠PEB=∠PDC,
∴∠PEB=∠PBC
∴PB=PE
∴△PBE为等腰三角形.
②EC=
| PC-PA | ||
|
证明:如图1,
过P作PF垂直于BC,过E作EA′∥PF交AC于A',
∵BF=EF,EA′∥PF∥AB,
∴PA=PA′,
在△A′EC中∠A′EC=90°,∠A′CE=45°,
∴△A′EC为等腰直角三角形,
∴A′C=
| 2 |
∴EC=
| PC-PA′ | ||
|
| PC-PA | ||
|
(2)结论①仍成立;
结论②不成立,此时②中三条线段的数量关系是EC=
| PA-PC | ||
|
点评:本题考查了正方形的性质,考查了等腰三角形的判定,本题中求证∠PEB=∠PBC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知⊙O1的半径r1=2,⊙O2的半径r2是方程
=
的根,当两圆相内切时,⊙O1与⊙O2的圆心距为( )
| 3 |
| x |
| 2 |
| x-1 |
| A、5 | B、4 | C、1或5 | D、1 |
 如图,是由三个相同的小正方体组成的几何体,该几何体的俯视图是( )
如图,是由三个相同的小正方体组成的几何体,该几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图,已知P为正方形ABCD内一点,以点B为旋转中心,将△ABP顺时针旋转使A点和C点重合,这时P点旋转至G点.
如图,已知P为正方形ABCD内一点,以点B为旋转中心,将△ABP顺时针旋转使A点和C点重合,这时P点旋转至G点.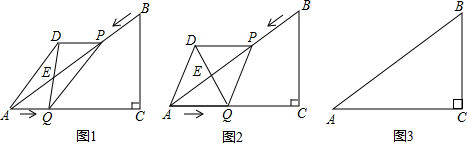
 如图,△ABC中∠BAC=60°,AB=2AC.点P在△ABC内,且PA=
如图,△ABC中∠BAC=60°,AB=2AC.点P在△ABC内,且PA=