题目内容
2.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC=70°.
(2)如图②,若∠A=100°,∠C=120°,则∠AEC=140°.
(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是∠AEC+∠A=180°+∠C.

分析 首先都需要过点E作EF∥AB,由AB∥CD,可得AB∥CD∥EF.
(1)根据两直线平行,内错角相等,即可求得∠AEC的度数;
(2)根据两直线平行,同旁内角互补,即可求得∠AEC的度数;
(3)根据两直线平行,内错角相等;两直线平行,同旁内角互补,即可求得结果.
解答 解:如图, 过点E作EF∥AB,
过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
(1)∵AB∥CD∥EF.
∴∠A=30°,∠C=40°,
∴∠1=∠A=30°,∠2=∠C=40°,
∴∠AEC=∠1+∠2=70°;
故答案为:70°;
(2)∵AB∥CD∥EF.
∴∠1+∠A=180°,∠2+∠C=180°,
∵∠A=100°,∠C=120°,
∴∠1+∠2+100°+120°=360°,
∴∠AEC=360°-100°-120°=140°;
故答案为:140°;
(3)∠AEC+∠A=180°+∠C;理由如下:
∵AB∥CD∥EF.
∴∠1+∠A=180°,∠2=∠C,
∴∠1=180°-∠A,
∴∠AEC=∠1+∠2=180°-∠A+∠C,
∴∠AEC+∠A=180°+∠C.
点评 此题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.解此题的关键是准确作出辅助线:作平行线,这是此类题目的常见解法.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
8.张大爷对自己生产的土特产进行试验加工后,分为甲、乙、丙三种不同包装推向市场进行销售,其相关信息如下表:
这三种不同包装的土特产每一种都销售了120千克.
(1)张大爷销售甲种包装的土特产赚了多少钱?
(2)销售乙、丙这两种包装的土特产总共赚了多少钱?(用含m、n的代数式表示)
(3)当m=2.8,n=3.7时,求第(2)题中的代数式的值;并说明该值所表示的实际意义.
| 重量(克/袋) | 销售价(元/袋) | 成本(元/袋) | |
| 甲 | 200 | 2.5 | 1.9 |
| 乙 | 300 | m | 2.9 |
| 丙 | 400 | n | 3.8 |
(1)张大爷销售甲种包装的土特产赚了多少钱?
(2)销售乙、丙这两种包装的土特产总共赚了多少钱?(用含m、n的代数式表示)
(3)当m=2.8,n=3.7时,求第(2)题中的代数式的值;并说明该值所表示的实际意义.
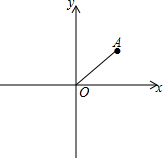 如图,在直角坐标系中,O是坐标原点,且点A坐标为(4,4),P是y轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,求P点的坐标.
如图,在直角坐标系中,O是坐标原点,且点A坐标为(4,4),P是y轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,求P点的坐标.
 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( ) 解不等式2(x+1)-1≥4x+3,并把它的解集在数轴上表示出来.
解不等式2(x+1)-1≥4x+3,并把它的解集在数轴上表示出来.